题目内容
过抛物线y2=4x的焦点,方向向量为(1,
)的直线方程是 .
| 3 |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:求出抛物线的焦点坐标,利用直线的方向向量即可求出直线方程.
解答:
解:∵抛物线的方程为y2=4x,
∴抛物线的焦点坐标为(1,0),
∵方向向量为(1,
),
∴直线的斜率k=
,
即直线的方程为y-0=
(x-1),
即
x-y-
=0;
故答案为:
x-y-
=0
∴抛物线的焦点坐标为(1,0),
∵方向向量为(1,
| 3 |
∴直线的斜率k=
| 3 |
即直线的方程为y-0=
| 3 |
即
| 3 |
| 3 |
故答案为:
| 3 |
| 3 |
点评:本题主要考查直线方程的求法,根据抛物线的定义求出焦点坐标即可,注意直线的方向向量和直线斜率之间的关系.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
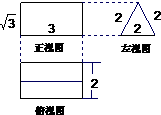 已知某个几何体的三视图如图所示,试根据图中所标出的尺寸(单位:cm),可得这个几何体的表面积是( )
已知某个几何体的三视图如图所示,试根据图中所标出的尺寸(单位:cm),可得这个几何体的表面积是( )A、18+
| ||
B、18+2
| ||
C、24+2
| ||
D、24+2
|