题目内容
分形几何学是数学家伯努瓦•曼得尔布罗在20世纪70年代创立的一门新的数学学科,它的创立为解决传统科学众多领域的难题提供了全新的思路.按照如图甲所示的分形规律可得如图乙所示的一个树形图:
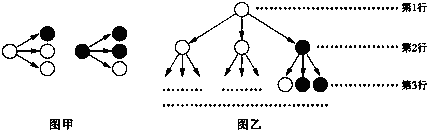
已知第三行有白圈5个,黑圈4个,我们采用“坐标”来表示各行中的白圈、黑圈的个数.比如第一行记为(1,0),第二行记为(2,1),第三行记为(5,4),则第四的白圈与黑圈的“坐标”为 .照此规律,第n行中的白圈、黑圈的“坐标”为 .

已知第三行有白圈5个,黑圈4个,我们采用“坐标”来表示各行中的白圈、黑圈的个数.比如第一行记为(1,0),第二行记为(2,1),第三行记为(5,4),则第四的白圈与黑圈的“坐标”为
考点:归纳推理
专题:推理和证明
分析:根据图甲所示的分形规律,1个白圈分形为2个白圈1个黑圈,1个黑圈分形为1个白圈2个黑圈,根据第三行的数据可求出第四行的“坐标”;
再根据前五行的白圈数乘以2,分别是2,4,10,28,82,即1+1,3+1,9+1,27+1,81+1,可归纳第n行的白圈数为
,黑圈数为
-1=
.
再根据前五行的白圈数乘以2,分别是2,4,10,28,82,即1+1,3+1,9+1,27+1,81+1,可归纳第n行的白圈数为
| 3n-1+1 |
| 2 |
| 3n-1+1 |
| 3 |
| 3n-1-1 |
| 3 |
解答:
解:根据图甲所示的分形规律,1个白圈分形为2个白圈1个黑圈,1个黑圈分形为1个白圈2个黑圈,
第一行记为(1,0),第二行记为(2,1),第三行记为(5,4),第四行的白圈数为2×5+4=14;黑圈数为5+2×4=13,
∴第四行的“坐标”为(14,13);
第五行的“坐标”为(41,40),
各行白圈数乘以2,分别是2,4,10,28,82,即1+1,3+1,9+1,27+1,81+1,
∴第n行的白圈数为
,黑圈数为
-1=
,
故答案是(14,13),(
,
)n∈N+.
第一行记为(1,0),第二行记为(2,1),第三行记为(5,4),第四行的白圈数为2×5+4=14;黑圈数为5+2×4=13,
∴第四行的“坐标”为(14,13);
第五行的“坐标”为(41,40),
各行白圈数乘以2,分别是2,4,10,28,82,即1+1,3+1,9+1,27+1,81+1,
∴第n行的白圈数为
| 3n-1+1 |
| 2 |
| 3n-1+1 |
| 3 |
| 3n-1-1 |
| 3 |
故答案是(14,13),(
| 3n-1+1 |
| 2 |
| 3n-1-1 |
| 2 |
点评:本题考查了归纳推理的应用,多观察几组数据是发现规律的有效方法.

练习册系列答案
相关题目
函数y=
的单调增区间是( )
| x2+2x-3 |
| A、[1,+∞) |
| B、(-∞,-1] |
| C、(-∞,-3] |
| D、[-3,-1] |