题目内容
5.函数f(x)=sin(x+2φ)-2sinφcos(x+φ)的最大值为( )| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
分析 利用积化和差公式将函数化为y=Asin(ωx+φ)的形式,结合三角函数的性质求解即可.
解答 解:函数f(x)=sin(x+2φ)-2sinφcos(x+φ),
化解可得:f(x)=sin(x+2φ)-2[$\frac{1}{2}$sin(x+2φ)-$\frac{1}{2}$sinx]=sinx.
根据正弦函数的性质可得:函数f(x)的最大值为:1.
故选D:
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进行化简是解决本题的关键.属于基础题.

练习册系列答案
相关题目
 如图,四棱锥P-ABCD中,PB⊥底面ABCD.底面ABCD为直角梯形,∠ABC=90°,AD∥BC,BC=2,AB=AD=PB=1,点E为棱PA的中点.
如图,四棱锥P-ABCD中,PB⊥底面ABCD.底面ABCD为直角梯形,∠ABC=90°,AD∥BC,BC=2,AB=AD=PB=1,点E为棱PA的中点. 如图,单摆的摆线离开平衡位置的位移S(厘米)和时间t(秒)的函数关系是S=$\frac{1}{2}$sin(2t+$\frac{π}{3}$),则摆球往复摆动一次所需要的时间是π秒.
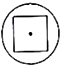
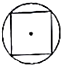
如图,单摆的摆线离开平衡位置的位移S(厘米)和时间t(秒)的函数关系是S=$\frac{1}{2}$sin(2t+$\frac{π}{3}$),则摆球往复摆动一次所需要的时间是π秒.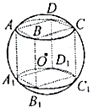 如图所示,几何体为一个球挖去一个内接正方体得到的组合体,现用一个经过球心的平面截它,所得的截面图形不可能是( )
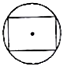
如图所示,几何体为一个球挖去一个内接正方体得到的组合体,现用一个经过球心的平面截它,所得的截面图形不可能是( )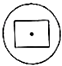
 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PD⊥平面ABCD,且AB=PD=2,则这个四棱锥的内切球半径是2-$\sqrt{2}$.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PD⊥平面ABCD,且AB=PD=2,则这个四棱锥的内切球半径是2-$\sqrt{2}$.