题目内容

10．如图，在四棱锥P-ABCD中，底面ABCD是正方形，PD⊥平面ABCD，且AB=PD=2，则这个四棱锥的内切球半径是2-$\sqrt{2}$．

分析 由题意球心到各个面的距离均相等，联想到用体积法求解．

解答 解：设球心为S，连SA、SB、SC、SD、SP，则把此四棱锥分为五个棱锥，设它们的高均为R
∵VP-ABCD=VS-PDA+VS-PDC+VS-ABCD+VS-PAB+VS-PBC
∴$\frac{1}{3}×2×2×2$=$\frac{1}{3}R（2×\frac{1}{2}×2×2+2×\frac{1}{2}×2×2\sqrt{2}）$，
∴R=2-$\sqrt{2}$．
故答案为：2-$\sqrt{2}$．

点评 本题主要考查棱锥的性质以及内切外接的相关知识点．“内切”和“外接”等有关问题，首先要弄清几何体之间的相互关系，主要是指特殊的点、线、面之间关系，然后把相关的元素放到这些关系中解决问题．

练习册系列答案
相关题目
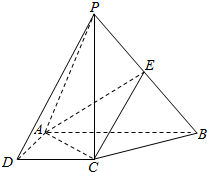20．如图，在四棱锥P-ABCD中，底面ABCD是直角梯形，AB⊥AD，AB∥CD，AB=2AD=2CD=2，BC=$\sqrt{2}$，且PC⊥CD，BC⊥PA，E是PB的中点．
（1）求证：平面PBC⊥平面EAC；
（2）若二面角P-AC-E的正弦值为$\frac{{\sqrt{3}}}{3}$，求直线PA与平面EAC所成角的余弦值．
1．若直线l：y=k（x+1）与圆C：（x-1）2+y2=1恒有公共点，则k的取值范围是$-\frac{{\sqrt{3}}}{3}≤k≤\frac{{\sqrt{3}}}{3}$，，直线l的倾斜角的取值范围是$θ∈[{0，\frac{π}{6}}]∪[{\frac{5π}{6}，π}）$．
18．在抛物线x2=2py（p＞0）上，纵坐标为2的点到抛物线焦点的距离为5，则p=6．
5．函数f（x）=sin（x+2φ）-2sinφcos（x+φ）的最大值为（　　）
A．2B．$\frac{3}{2}$C．$\frac{1}{2}$D．1
15．在平面直角坐标系xOy中，设圆C的方程为（x-a）2+（y-2a+4）2=1．
（Ⅰ）若圆C经过A（3，3）与B（4，2）两点，求实数a的值；
（Ⅱ）点P（0，3），若圆C上存在点M，使|MP|=2|MO|，求实数a的取值范围．
2．已知函数f（x）=（1-x）ex．
（1）证明：当x＞0时，f（x）＜f（-x）；
（2）若方程f（x）=a（1+x2）有两个不相等的实根x1，x2，求实数a的取值范围，并证明：x1+x2＜0．
19．已知A，B是抛物线y2=4x上异于原点O的两点，且$\overrightarrow{OA}•\overrightarrow{OB}=0$
（1）求证：直线AB恒过定点（4，0）
（2）若将$\overrightarrow{OA}•\overrightarrow{OB}=0$改为$\overrightarrow{OA}•\overrightarrow{OB}=m（m≠0）$，判断直线AB是否经过一定点．若是，请写出m=-2时该定点的坐标（直接写出结论即可）
20．已知直线l：$\left\{\begin{array}{l}x=1+\frac{1}{2}t\\ y=\frac{{\sqrt{3}}}{2}t\end{array}\right.$（t为参数），曲线C1：x2+y2=1
（1）设l与C1相交于A，B两点，求|AB|．
（2）若曲线C1上各点的横坐标压缩为原来的$\frac{1}{2}$，纵坐标压缩为原来的$\frac{{\sqrt{3}}}{2}$，得到曲线C2，设点P是曲线C2上的一个动点，求它到直线l的距离的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网