题目内容
6．
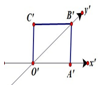如图所示正方形O'A'B'C'的边长为2cm，它是一个水平放置的一个平面图形的直观图，则原图形的周长是16cm，面积是$8\sqrt{2}c{m^2}$．
分析 根据斜二测画法画直观图的性质，即平行性不变，平行于x轴的线段长度不变，平行于y轴的线段的长度减半，结合图形求得原图形的各边长，可得周长、面积．
解答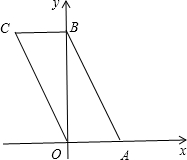 
解：∵直观图正方形O′A′B′C′的边长2cm，∴O′B′=2$\sqrt{2}$，
原图形为平行四边形OABC，其中OA=2，高OB=4$\sqrt{2}$．
∴AB=CO=$\sqrt{32+4}$=6．
∴原图形的周长L=2×6+2×2=16（cm），面积是2×$4\sqrt{2}$=8$\sqrt{2}$cm2
故答案为16cm，$8\sqrt{2}c{m^2}$．
点评 本题考查了画平面图形直观图的斜二测画法，熟练掌握斜二测画法的特征是解题的关键．
练习册系列答案
相关题目
16．在正方体ABCD-A1B1C1D1中，E，F分别为CC1和BB1的中点，则异面直线AE与D1F所成角的余弦值为（ ）
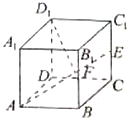
| A． | 0 | B． | $\frac{{\sqrt{3}}}{12}$ | C． | $\frac{{\sqrt{3}}}{3}$ | D． | $\frac{1}{9}$ |
1．设有四个命题，其中真命题的个数是（ ）
①有两个平面互相平行，其余各面都是四边形的多面体一定是棱柱；
②有一个面是多边形，其余各面都是三角形的多面体一定是棱锥；
③用一个面去截棱锥，底面与截面之间的部分叫棱台；
④侧面都是长方形的棱柱叫长方体．
①有两个平面互相平行，其余各面都是四边形的多面体一定是棱柱；
②有一个面是多边形，其余各面都是三角形的多面体一定是棱锥；
③用一个面去截棱锥，底面与截面之间的部分叫棱台；
④侧面都是长方形的棱柱叫长方体．
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |
15．直线mx+$\frac{n}{2}$y-1=0在y轴上的截距是-1，且它的倾斜角是直线$\sqrt{3}x-y-3\sqrt{3}$=0的倾斜角的2倍，则（ ）
| A． | m=-$\sqrt{3}$，n=-2 | B． | m=$\sqrt{3}$，n=2 | C． | m=$\sqrt{3}$，n=-2 | D． | m=-$\sqrt{3}$，n=2 |