题目内容
17.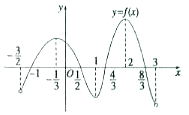 函数y=f(x)在其定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示,记y=f(x)的导函数为y=f'(x),则不等式f′(x)≤0的解集是[-$\frac{1}{3}$,1]∪[2,3).
函数y=f(x)在其定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示,记y=f(x)的导函数为y=f'(x),则不等式f′(x)≤0的解集是[-$\frac{1}{3}$,1]∪[2,3).
分析 不等式的解集为函数f(x)的减区间.
解答 解:由图象可知f(x)在区间[-$\frac{1}{3}$,1]和[2,3)上单调递减,
∴f′(x)≤0的解集为[-$\frac{1}{3}$,1]∪[2,3).
故答案为:[-$\frac{1}{3}$,1]∪[2,3).
点评 本题考查了导数与函数单调性的关系,属于中档题.

练习册系列答案
相关题目
5.设函数y=f(x)的定义域为D,若对于任意x1,x2∈D,当x1+x2=2a时,恒有f(x1)+f(x2)=2b,则称点(a,b)为函数y=f(x)图象的对称中心.研究函数f(x)=x+sinπx-3的某一个对称中心,并利用对称中心的上述定义,可得到$f(\frac{1}{2017})+f(\frac{2}{2017})+f(\frac{3}{2017})+…+f(\frac{4032}{2017})+f(\frac{4033}{2017})$的值为( )
| A. | -4033 | B. | 4033 | C. | 8066 | D. | -8066 |
9.已知P,A,B是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$上不同的三点,且A,B关于原点对称,若直线PA,PB的斜率乘积${k_{PA}}•{k_{PB}}=\frac{3}{4}$,则该双曲线的离心率是( )
| A. | 2 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{7}}}{2}$ | D. | $2\sqrt{2}$ |
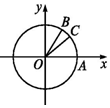 在如图所示的直角坐标系xOy中,点A,B是单位圆上的点,且A(1,0),∠AOB=$\frac{π}{3}$.现有一动点C在单位圆的劣弧$\widehat{AB}$上运动,设∠AOC=α.
在如图所示的直角坐标系xOy中,点A,B是单位圆上的点,且A(1,0),∠AOB=$\frac{π}{3}$.现有一动点C在单位圆的劣弧$\widehat{AB}$上运动,设∠AOC=α.