题目内容
已知点P（3，4）和圆C：（x-2）2+y2=4，A，B是圆C上两个动点，且|AB|=2
，则
•（
+
）（O为坐标原点）的取值范围是（ ）
| 3 |
| OP |
| OA |
| OB |
| A、[3，9] |
| B、[1，11] |
| C、[6，18] |
| D、[2，22] |
考点：平面向量数量积的运算,圆的标准方程
专题：直线与圆
分析：设线段AB的中点为D，可得
=|CD|，即点D在圆：（x-2）2+y2=1上，可设点D（2+cosα，sinα），
求得
•（
+
）=
•2
=12+10sin（α+θ），可得
•（
+
）的范围．
| 3 |
求得
| OP |
| OA |
| OB |
| OP |
| OD |
| OP |
| OA |
| OB |
解答：
解：设线段AB的中点为D，∵|AB|=2
，∴|AD|=
，
则|CD|=1，即D的轨迹以C为圆心半径为1的圆，
即点D在圆（x-2）2+y2=1上，可设点D（2+cosα，sinα），
则
•（
+
）=
•2
=（6，8）•（2+cosα，sinα）=12+6cosα+8sinα
=12+10sin（α+θ），其中，sinθ=
，cosθ=
，
∴
•（
+
）的最小值为12-10=2，最大值为12+10=22，
∴
•（
+
）的范围是[2，22]．
故选：D．
| 3 |
| 3 |
则|CD|=1，即D的轨迹以C为圆心半径为1的圆，
即点D在圆（x-2）2+y2=1上，可设点D（2+cosα，sinα），
则
| OP |
| OA |
| OB |
| OP |
| OD |
=12+10sin（α+θ），其中，sinθ=
| 3 |
| 5 |
| 4 |
| 5 |
∴
| OP |
| OA |
| OB |
∴
| OP |
| OA |
| OB |
故选：D．
点评：本题主要考查直线和圆相交的性质，辅助角公式的应用，两个向量的数量积的运算，属于中档题．
练习册系列答案
相关题目
定义在R上的函数f（x），恒有|f（-x）|=|f（x）|，则函数f（x）为（ ）
| A、奇函数 |
| B、偶函数 |
| C、奇函数或偶函数 |
| D、可能既不是奇函数，也不是偶函数 |
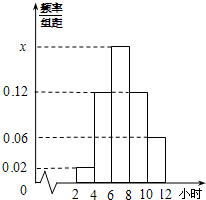某校为了解学生寒假期间的学习情况，从初中及高中各班共抽取了50名学生，对他们每天平均学习时间进行统计．请根据下面的各班人数统计表和学习时间的频率分布直方图解决下列问题：