题目内容
设关于x的一元二次方程x2+2ax+b2=0.
(Ⅰ)若a,b都是从集合{1,2,3,4}中任取的数字,求方程有实根的概率;
(Ⅱ)若a是从区间[0,4]中任取的数字,b是从区间[1,4]中任取的数字,求方程有实根的概率.
(Ⅰ)若a,b都是从集合{1,2,3,4}中任取的数字,求方程有实根的概率;
(Ⅱ)若a是从区间[0,4]中任取的数字,b是从区间[1,4]中任取的数字,求方程有实根的概率.
考点:古典概型及其概率计算公式,几何概型
专题:概率与统计
分析:(Ⅰ)列举所有的情况,找出方程有实根的事件包含的基本事件个数,利用古典概型概率公式计算即可;
(Ⅱ)画出a是从区间[0,4]中任取的数字,b是从区间[1,4]中任取的数字的可行域,找出方程有实根的事件所代表的平面区域,利用几何概型概率公式计算即可.
(Ⅱ)画出a是从区间[0,4]中任取的数字,b是从区间[1,4]中任取的数字的可行域,找出方程有实根的事件所代表的平面区域,利用几何概型概率公式计算即可.
解答:
 解:(I)设事件A为“方程有实根”,
解:(I)设事件A为“方程有实根”,
记(a,b)为取到的一种组合,则所有的情况有:
(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),
(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4).
一共16种且每种情况被取到的可能性相同.
∵关于x的一元二次方程x2+2ax+b2=0有实根,
∴△=4a2-4b2≥0,
∴a≥b.
∴事件A包含的基本事件有:
(1,1),(2,1),(2,2),(3,1),(3,2),(3,3),(4,1),(4,2),
(4,3),(4,4)共10种.
∴P(A)=
=
.
∴方程有实根的概率是
.
(Ⅱ)设事件B=“方程有实根”,记(a,b)为取到的一种组合.
∵a是从区间[0,4]中任取的数字,b是从区间[1,4]中任取的数字,
∴点(a,b)所在区域是长为4,宽为3的矩形区域.
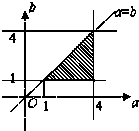
又∵满足a≥b的点的区域是如图所示的阴影部分.
∴P(B)=
=
.
∴方程有实根的概率是
.
 解:(I)设事件A为“方程有实根”,
解:(I)设事件A为“方程有实根”,记(a,b)为取到的一种组合,则所有的情况有:
(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),
(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4).
一共16种且每种情况被取到的可能性相同.
∵关于x的一元二次方程x2+2ax+b2=0有实根,
∴△=4a2-4b2≥0,
∴a≥b.
∴事件A包含的基本事件有:
(1,1),(2,1),(2,2),(3,1),(3,2),(3,3),(4,1),(4,2),
(4,3),(4,4)共10种.
∴P(A)=
| 10 |
| 16 |
| 5 |
| 8 |
∴方程有实根的概率是
| 5 |
| 8 |
(Ⅱ)设事件B=“方程有实根”,记(a,b)为取到的一种组合.
∵a是从区间[0,4]中任取的数字,b是从区间[1,4]中任取的数字,
∴点(a,b)所在区域是长为4,宽为3的矩形区域.
又∵满足a≥b的点的区域是如图所示的阴影部分.
∴P(B)=
| ||
| 3×4 |
| 3 |
| 8 |
∴方程有实根的概率是
| 3 |
| 8 |
点评:本题考查古典概型和几何概型的概率计算,以及一元二次方程根的判别式的应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设f(x)=|lnx|,若函数g(x)=f(x)-ax在区间(0,3]上有三个零点,则实数a的取值范围是( )
A、(0,
| ||||
B、(
| ||||
C、(0,
| ||||
D、[
|
已知点P(3,4)和圆C:(x-2)2+y2=4,A,B是圆C上两个动点,且|AB|=2
,则
•(
+
)(O为坐标原点)的取值范围是( )
| 3 |
| OP |
| OA |
| OB |
| A、[3,9] |
| B、[1,11] |
| C、[6,18] |
| D、[2,22] |