题目内容
4.已知函数f(x)=3x-($\frac{1}{3}$)x,则f(x)( )| A. | 是偶函数,且在R上是增函数 | B. | 是奇函数,且在R上是增函数 | ||
| C. | 是偶函数,且在R上是减函数 | D. | 是奇函数,且在R上是减函数 |
分析 由已知得f(-x)=-f(x),即函数f(x)为奇函数,由函数y=3x为增函数,y=($\frac{1}{3}$)x为减函数,结合“增”-“减”=“增”可得答案.
解答 解:f(x)=3x-($\frac{1}{3}$)x=3x-3-x,
∴f(-x)=3-x-3x=-f(x),
即函数f(x)为奇函数,
又由函数y=3x为增函数,y=($\frac{1}{3}$)x为减函数,
故函数f(x)=3x-($\frac{1}{3}$)x为增函数,
故选:B.
点评 本题考查的知识点是函数的奇偶性,函数的单调性,是函数图象和性质的综合应用,难度不大,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.下列各式的运算结果为纯虚数的是( )
| A. | i(1+i)2 | B. | i2(1-i) | C. | (1+i)2 | D. | i(1+i) |
19.设x、y、z为正数,且2x=3y=5z,则( )
| A. | 2x<3y<5z | B. | 5z<2x<3y | C. | 3y<5z<2x | D. | 3y<2x<5z |
9.复平面内表示复数z=i(-2+i)的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.下列命题为真命题的是( )
| A. | 若p∧q为假命题,则p∨q为真命题 | |
| B. | 不存在实数α,β,使得等式tanα+tanβ=tan(α+β)成立 | |
| C. | 函数f(x)=ax2+bx+c为偶函数的充要条件是 b=0 | |
| D. | 若定义在R上的函数f(x)满足f(x)•f(x+1)=1,则f(x)是一个周期为1的函数 |
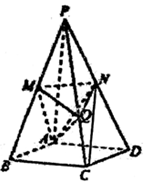 如图,在四棱锥P-ABCD中,底面是边长为2$\sqrt{3}$的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=2$\sqrt{6}$,M、N分别为PB,PD的中点.
如图,在四棱锥P-ABCD中,底面是边长为2$\sqrt{3}$的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=2$\sqrt{6}$,M、N分别为PB,PD的中点.