题目内容
5．已知集合A={x|-1＜x＜2}，B={-1，0，1}，A∩B={0，1}．分析 直接根据交集的定义即可求出．
解答 解：集合A={x|-1＜x＜2}，B={-1，0，1}，
则A∩B={0，1}，
故答案为：{0，1}．
点评 本题考查集合的交集的运算运算，解题时要认真审题，属于基础题．
练习册系列答案
相关题目
17．已知命题p：?x＞0，sinx＞-1；q：?x＞0，cosx＞-1，则下列命题是真命题的是（ ）
| A． | p∧q | B． | p∨（￢q） | C． | （￢p）∨q | D． | ￢（p∨q） |
13．若A={x|x2+2x-8＜0}，B={x|x＜1}，则图中阴影部分表示的集合为（ ）
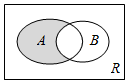
| A． | （-4，1] | B． | （1，2） | C． | [1，2） | D． | （-4，1） |
20．已知i是虚数单位，则复数$\frac{{{{（{1-i}）}^2}}}{1+i}$在复平面内对应的点在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
10．
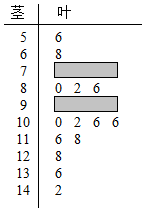某校高三期中考试后，数学教师对本次全部数学成绩按1：20进行分层抽样，随机抽取了20名学生的成绩为样本，成绩用茎叶图记录如图所示，但部分数据不小心丢失，同时得到如表所示的频率分布表：
（Ⅰ）求表中a，b的值及成绩在[90，110）范围内的个体数；
（Ⅱ）从样本中成绩在[100，130）内的个体中随机抽取4个个体，设其中成绩在[100，110）内的个体数为X，求X的分布列及数学期望E（X）；
（Ⅲ）若把样本各分数段的频率看作总体相应各分数段的概率，现从全校高三期中考试数学成绩中随机抽取3个，求其中恰好有1个成绩及格的概率（成绩在[90，150）内为及格）．
附注：假定逐次抽取，且各次抽取互相独立．
某校高三期中考试后，数学教师对本次全部数学成绩按1：20进行分层抽样，随机抽取了20名学生的成绩为样本，成绩用茎叶图记录如图所示，但部分数据不小心丢失，同时得到如表所示的频率分布表：| 分数段（分） | [50，70） | [70，90） | [90，110） | [110，130） | [130，150） | 总计 |
| 频数 | b | |||||
| 频率 | a | 0.25 |
（Ⅱ）从样本中成绩在[100，130）内的个体中随机抽取4个个体，设其中成绩在[100，110）内的个体数为X，求X的分布列及数学期望E（X）；
（Ⅲ）若把样本各分数段的频率看作总体相应各分数段的概率，现从全校高三期中考试数学成绩中随机抽取3个，求其中恰好有1个成绩及格的概率（成绩在[90，150）内为及格）．
附注：假定逐次抽取，且各次抽取互相独立．
14．设集合A={-2，-1，0，1，2}，集合B={y=|y=log${\;}_{\frac{1}{2}}$x，x≥1}，A∩B=（ ）
| A． | {1，2} | B． | {-2，-1} | C． | {-2，-1，0} | D． | {1，2，0} |
15．设x是虚数单位，如果复数$\frac{a+i}{2-i}$的实部与虚部相等，那么实数a的值为（ ）
| A． | $\frac{1}{3}$ | B． | $-\frac{1}{3}$ | C． | 3 | D． | -3 |