题目内容
10.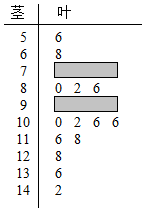 某校高三期中考试后,数学教师对本次全部数学成绩按1:20进行分层抽样,随机抽取了20名学生的成绩为样本,成绩用茎叶图记录如图所示,但部分数据不小心丢失,同时得到如表所示的频率分布表:
某校高三期中考试后,数学教师对本次全部数学成绩按1:20进行分层抽样,随机抽取了20名学生的成绩为样本,成绩用茎叶图记录如图所示,但部分数据不小心丢失,同时得到如表所示的频率分布表:| 分数段(分) | [50,70) | [70,90) | [90,110) | [110,130) | [130,150) | 总计 |
| 频数 | b | |||||
| 频率 | a | 0.25 |
(Ⅱ)从样本中成绩在[100,130)内的个体中随机抽取4个个体,设其中成绩在[100,110)内的个体数为X,求X的分布列及数学期望E(X);
(Ⅲ)若把样本各分数段的频率看作总体相应各分数段的概率,现从全校高三期中考试数学成绩中随机抽取3个,求其中恰好有1个成绩及格的概率(成绩在[90,150)内为及格).
附注:假定逐次抽取,且各次抽取互相独立.
分析 (Ⅰ)由茎叶图知成绩在[50,70)范围内的有2 人,成绩在[110,130)范围内的有3人,由此能求出表中a,b的值及成绩在[90,110)范围内的个体数.
(Ⅱ)由茎叶图知成绩在[100,130)内的共有7人,其中成绩在[100,110)内的共有4人,于是X的可能取值为1,2,3,4,分别求出相应的概率,由此能求出X的分布列及数学期望E(X).
(Ⅲ)该校高三期中考试数学及格率为p=1-0.1-0.25=0.65,设随机抽取3个,其中恰有一个成绩及格的事件为A,由此能求出恰好有1个成绩及格的概率.
解答 解:(Ⅰ)由茎叶图知成绩在[50,70)范围内的有2 人,
成绩在[110,130)范围内的有3人,
∴a=$\frac{2}{20}$=0.1,b=3,
成绩在[90,110)范围内的频率为:1-0.1-0.25-0.25=0.4,
∴成绩在[90,110)范围内的样本数为20×0.4=8.
(Ⅱ)由茎叶图知成绩在[100,130)内的共有7人,其中成绩在[100,110)内的共有4人,
于是X的可能取值为1,2,3,4,
P(X=1)=$\frac{{C}_{4}^{1}{C}_{3}^{3}}{{C}_{7}^{4}}$=$\frac{4}{35}$,
P(X=2)=$\frac{{C}_{4}^{2}{C}_{3}^{2}}{{C}_{7}^{4}}$=$\frac{18}{35}$,
P(X=3)=$\frac{{C}_{4}^{3}{C}_{3}^{1}}{{C}_{7}^{4}}$=$\frac{12}{35}$,
P(X=4)=$\frac{{C}_{4}^{4}{C}_{3}^{0}}{{C}_{7}^{4}}$=$\frac{1}{35}$,
∴X的分布列为:
| X | 1 | 2 | 3 | 4 |
| P | $\frac{4}{35}$ | $\frac{18}{35}$ | $\frac{12}{35}$ | $\frac{1}{35}$ |
(Ⅲ)该校高三期中考试数学及格率为p=1-0.1-0.25=0.65,
设随机抽取3个,其中恰有一个成绩及格的事件为A,则根据题设有:
P(A)=${C}_{3}^{1}×0.65×(1-0.65)^{2}$=0.238875.
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

 阅读快车系列答案
阅读快车系列答案| A. | 3n(2n-1) | B. | 3n(2n+1) | C. | $\frac{3n(n+1)}{2}$ | D. | $\frac{3n(n-1)}{2}$ |
| A. | 4 | B. | $2\sqrt{2}$ | C. | 8 | D. | 16 |
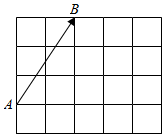 如图,在4×5的方格纸中有一个向量$\overrightarrow{AB}$(每个小方格都是单位小正方形),分别以图中的格点为起点和终点作向量,其中与$\overrightarrow{AB}$相等的向量有7个,与$\overrightarrow{AB}$相反的向量有8个;与$\overrightarrow{AB}$长度相等的共线向量有15个($\overrightarrow{AB}$除外);与$\overrightarrow{AB}$方向相同且模为5的向量有3个.
如图,在4×5的方格纸中有一个向量$\overrightarrow{AB}$(每个小方格都是单位小正方形),分别以图中的格点为起点和终点作向量,其中与$\overrightarrow{AB}$相等的向量有7个,与$\overrightarrow{AB}$相反的向量有8个;与$\overrightarrow{AB}$长度相等的共线向量有15个($\overrightarrow{AB}$除外);与$\overrightarrow{AB}$方向相同且模为5的向量有3个.