题目内容
17.已知命题p:?x>0,sinx>-1;q:?x>0,cosx>-1,则下列命题是真命题的是( )| A. | p∧q | B. | p∨(¬q) | C. | (¬p)∨q | D. | ¬(p∨q) |
分析 根据条件判断命题p,q的真假,结合复合命题真假关系进行判断即可.
解答 解:?x>0,sinx>-1不成立,故p是假命题,
当x=$\frac{π}{3}$时,cosx=$\frac{1}{2}$,满足cosx>-1成立,即q是真命题,
则p∧q为假命题,p∨(¬q)为假命题,(¬p)∨q为真命题.¬(p∨q)为假命题.
故选:C
点评 本题主要考查复合命题真假的关系的判断,根据条件判断命题p,q的真假是解决本题的关键.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
4.若双曲线M上存在四个点A,B,C,D,使得四边形ABCD是正方形,则双曲线M的离心率的取值范围是( )
| A. | $({\sqrt{2},+∞})$ | B. | $({\sqrt{2},2})$ | C. | $({2,2+\sqrt{2}})$ | D. | $({\sqrt{5},+∞})$ |
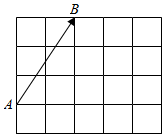 如图,在4×5的方格纸中有一个向量$\overrightarrow{AB}$(每个小方格都是单位小正方形),分别以图中的格点为起点和终点作向量,其中与$\overrightarrow{AB}$相等的向量有7个,与$\overrightarrow{AB}$相反的向量有8个;与$\overrightarrow{AB}$长度相等的共线向量有15个($\overrightarrow{AB}$除外);与$\overrightarrow{AB}$方向相同且模为5的向量有3个.
如图,在4×5的方格纸中有一个向量$\overrightarrow{AB}$(每个小方格都是单位小正方形),分别以图中的格点为起点和终点作向量,其中与$\overrightarrow{AB}$相等的向量有7个,与$\overrightarrow{AB}$相反的向量有8个;与$\overrightarrow{AB}$长度相等的共线向量有15个($\overrightarrow{AB}$除外);与$\overrightarrow{AB}$方向相同且模为5的向量有3个.