题目内容
20.已知i是虚数单位,则复数$\frac{{{{({1-i})}^2}}}{1+i}$在复平面内对应的点在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 由复数代数形式的乘除运算化简复数$\frac{{{{({1-i})}^2}}}{1+i}$,求出在复平面内对应的点的坐标,则答案可求.
解答 解:由$\frac{{{{({1-i})}^2}}}{1+i}$=$\frac{-2i(1-i)}{(1+i)(1-i)}=-1-i$,
则复数$\frac{{{{({1-i})}^2}}}{1+i}$在复平面内对应的点的坐标为:(-1,-1),位于第三象限.
故选:C.
点评 本题考查了复数代数形式的乘除运算,考查了复数的代数表示法及其几何意义,是基础题.

练习册系列答案
相关题目
15.根据如下样本数据
求得y关于x的线性回归直线方程为$\widehat{y}$=2.1x+0.85,则m的值为0.5.
| x | 0 | 1 | 4m | 3 |
| y | m | 3 | m+5 | 7 |
9.若集合A={0,1,2,4},B={1,2,3},则A∪B=( )
| A. | {1,2} | B. | {0,3,4} | C. | {0,1,2,3,4} | D. | {0,1,1,2,2,3,4} |
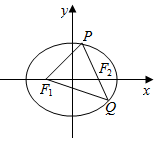 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的短轴长为2$\sqrt{3}$,且离心率e=$\frac{1}{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的短轴长为2$\sqrt{3}$,且离心率e=$\frac{1}{2}$.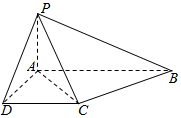 在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AB∥CD,且PA=AD=CD=a,AB=2a.求:
在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AB∥CD,且PA=AD=CD=a,AB=2a.求: