题目内容
7.双曲线$\frac{x^2}{a^2}-\frac{y^2}{7}=1$(a>0)的右焦点为圆(x-4)2+y2=1的圆心,则此双曲线的离心率为$\frac{4}{3}$.分析 求出双曲线的焦点坐标,圆的圆心坐标,列出方程,求解即可.
解答 解:双曲线$\frac{x^2}{a^2}-\frac{y^2}{7}=1$(a>0)的右焦点($\sqrt{{a}^{2}+7}$,0),为圆(x-4)2+y2=1的圆心(4,0).
由题意可得$\sqrt{{a}^{2}+7}=4$,解得a=3,则c=4,双曲线的离心率为:$\frac{c}{a}=\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 本题考查双曲线的简单性质与圆的方程的应用,考查计算能力.

练习册系列答案
相关题目
17.设命题P:?x∈R,x2+2>0.则¬P为( )
| A. | $?{x_0}∈R,{x_0}^2+2>0$ | B. | $?{x_0}∈R,{x_0}^2+2≤0$ | ||
| C. | $?{x_0}∈R,{x_0}^2+2<0$ | D. | ?x∈R,x2+2≤0 |
18.抛掷一枚质地均匀的骰子,向上的一面出现任意一种点数的概率都是$\frac{1}{6}$,记事件A为“向上的点数是奇数”,事件B为“向上的点数不超过3”,则概率P(A∪B)=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
2.已知实数x,y满足$\left\{\begin{array}{l}x+y≥3\\ x-y≤2\\ y≤2.\end{array}\right.$那么z=2x+y的最小值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
12.“k=1”是“直线$kx-y-3\sqrt{2}=0$与圆x2+y2=9相切”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
19.抛物线y=4x2的焦点到准线的距离是( )
| A. | 4 | B. | 2 | C. | $\frac{1}{8}$ | D. | $\frac{1}{16}$ |
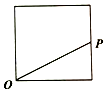 点P从点O出发,按逆时针方向沿周长为l的正方形运动一周,记O,P两点连线的距离y与点P走过的路程x为函数f(x),则y=f(x)的图象大致是( )
点P从点O出发,按逆时针方向沿周长为l的正方形运动一周,记O,P两点连线的距离y与点P走过的路程x为函数f(x),则y=f(x)的图象大致是( )