题目内容
19．抛物线y=4x2的焦点到准线的距离是（ ）| A． | 4 | B． | 2 | C． | $\frac{1}{8}$ | D． | $\frac{1}{16}$ |
分析 直接利用抛物线方程求解即可．
解答 解：抛物线y=4x2，即x2=$\frac{1}{4}$y的焦点到准线的距离为：p=$\frac{1}{8}$．
故选：C．
点评 本题考查抛物线的简单性质的应用，基本知识的考查．
练习册系列答案
相关题目
10．已知动直线y=k（x+1）与椭圆C：x2+3y2=5相交于A、B两点，已知点$M（-\frac{7}{3}，0）$，则$\overrightarrow{MA}•\overrightarrow{MB}$的值是（ ）
| A． | $-\frac{9}{4}$ | B． | $\frac{9}{4}$ | C． | $-\frac{4}{9}$ | D． | $\frac{4}{9}$ |
14．已知x，y∈R，且x＞y＞0，则（ ）
| A． | tanx-tany＞0 | B． | xsinx-ysiny＞0 | C． | lnx+lny＞0 | D． | 2x-2y＞0 |
11．正方体ABCD-A1B1C1D1中，二面角A-BD1-B1的大小是（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{π}{6}$ | C． | $\frac{2π}{3}$ | D． | $\frac{5π}{6}$ |
8．已知m，n是两条不同的直线，α，β是两个不同的平面（ ）
| A． | 若m∥α，m∥β，则α∥β | B． | 若m⊥α，m∥β，则α∥β | C． | 若m⊥α，n∥α，则m∥n | D． | 若m⊥α，n⊥α，则m∥n |
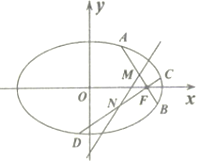已知椭圆$Ω：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$，过点$Q（{\frac{{\sqrt{2}}}{2}，1}）$作圆x2+y2=1的切线，切点分别为S，T．直线ST恰好经过Ω的右顶点和上顶点．