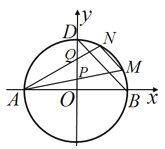题目内容
【题目】设椭圆![]() 的离心率为
的离心率为![]() ,左顶点到直线
,左顶点到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线![]() 与椭圆C相交于A、B两点,若以AB为直径的圆经过坐标原点O,试探究:点O到直线AB的距离是否为定值?若是,求出这个定值;否则,请说明理由;
与椭圆C相交于A、B两点,若以AB为直径的圆经过坐标原点O,试探究:点O到直线AB的距离是否为定值?若是,求出这个定值;否则,请说明理由;
(Ⅲ)在(Ⅱ)的条件下,试求△AOB面积S的最小值.
【答案】(1)![]() (2)见解析;(3)
(2)见解析;(3)![]()
【解析】
(Ⅰ)由已知,根据点到直线的距离公式,求解![]() ,再由椭圆的离心率,求得
,再由椭圆的离心率,求得![]() ,进而可求得椭圆的方程;
,进而可求得椭圆的方程;
(Ⅱ)法一:设![]() ,
,![]() ,①当直线l的斜率不存在时,求得点O到直线AB的距离为定值;②当直线l的斜率存在时,设其方程为
,①当直线l的斜率不存在时,求得点O到直线AB的距离为定值;②当直线l的斜率存在时,设其方程为![]() 联立方程组,根据根与系数的关系和题设条件,化简得
联立方程组,根据根与系数的关系和题设条件,化简得![]() ,进而求得点O到直线AB的距离为定值.
,进而求得点O到直线AB的距离为定值.
法二:设直线方程为![]() ,联立方程组,利用根与系数的关系和题设条件,化简得
,联立方程组,利用根与系数的关系和题设条件,化简得![]() ,进而得到点O到直线AB的距离为定值;
,进而得到点O到直线AB的距离为定值;
(Ⅲ)法一:当直线OA、直线OB斜率存在且不为0时,设直线OA的斜率为k,联立方程组,进而求得面积的表达式,利用基本不等式,即可求解面积的最小值;
法二:由(Ⅱ),①当直线l的斜率不存在时,![]() ,②当直线l的斜率存在时,得出面积的表示,利用基本不等式求得最小值,即可得到答案.
,②当直线l的斜率存在时,得出面积的表示,利用基本不等式求得最小值,即可得到答案.
(Ⅰ)由已知,![]() )
)
因为![]() 故所求椭圆的方程为
故所求椭圆的方程为![]() ;
;
(Ⅱ)法一:设![]() ,
,![]() ,
,
①当直线l的斜率不存在时,由椭圆对称性知![]() ,
,![]() ,因为以AB为直径的圆经过坐标原点O,故
,因为以AB为直径的圆经过坐标原点O,故![]() ,即
,即![]()
又因为点![]() 在椭圆上,故
在椭圆上,故![]() ,解得
,解得![]() ,
,
此时点O到直线AB的距离为![]()
②当直线l的斜率存在时,设其方程为![]() .
.
联立![]() 得:
得:![]()
所以![]() ,
,
由已知,以AB为直径的圆经过坐标原点O,则![]() ,且
,且![]()
故![]()
化简得![]() ,
,
故点O到直线AB的距离为![]() 综上,点O到直线AB的距离为定值
综上,点O到直线AB的距离为定值![]()
法二:(若设直线方程为![]() ,也要对直线斜率为0进行讨论)
,也要对直线斜率为0进行讨论)
设![]() ,
,
①当直线l的斜率为0时,由椭圆对称性知x1=-x2,y1=y2,因为以AB为直径的圆经过坐标原点O,故![]() ,即
,即![]()
又因为点![]() 在椭圆上,故
在椭圆上,故![]() ,解得
,解得![]() ,
,
此时点O到直线AB的距离为![]()
②当直线l的斜率不为0,或斜率不存在时,设其方程为![]() .
.
联立![]() 得:
得:![]()
所以![]() ,
,
故![]() ,
,
即![]() ,所以
,所以![]() ,
,
所以![]() ,
,
化简得![]() ,故点O到直线AB的距离为
,故点O到直线AB的距离为![]()
综上,点O到直线AB的距离为定值![]()
(Ⅲ)法一:当直线OA、直线OB中有一条斜率不存在,另一条斜率为0时,易知S=1;
当直线OA、直线OB斜率存在且不为0时,设直线OA的斜率为k,
则直线OB的斜率为![]() ,由
,由![]() 得
得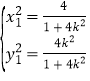 ,
,
同理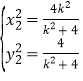 故
故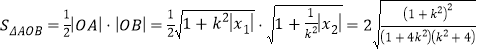
令![]() ,则
,则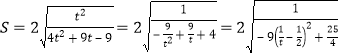
故![]() 综上,△AOB面积S的最小值为
综上,△AOB面积S的最小值为![]() .
.
法二:由(Ⅱ),①当直线l的斜率不存在时,![]() ,
,
②当直线l的斜率存在时,![]() ,且点O到直线AB的距离为
,且点O到直线AB的距离为![]() ,
,
![]()
![]()
故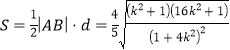 ,
,
令![]() ,则
,则![]() ,
,
因为![]() ,故
,故![]() .综上,△AOB面积S的最小值为
.综上,△AOB面积S的最小值为![]() .
.

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案