Question

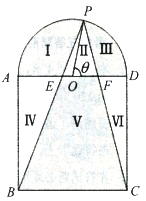
【题目】如图，某小区中央广场由两部分组成，一部分是边长为的正方形，另一部分是以为直径的半圆，其圆心为.规划修建的条直道， ， 将广场分割为个区域：Ⅰ、Ⅲ、Ⅴ为绿化区域（图中阴影部分），Ⅱ、Ⅳ、Ⅵ为休闲区域，其中点在半圆弧上， 分别与， 相交于点， .（道路宽度忽略不计）

（1）若经过圆心，求点到的距离；

（2）设， .

①试用表示的长度；

②当为何值时，绿化区域面积之和最大.

Answer 1

【答案】（1）（2）①最小值为②当时，绿化区域Ⅰ、Ⅲ、Ⅴ的面积之和最大

【解析】试题分析：（1）先建立直角坐标系，联立直线OB方程与圆方程解得P点纵坐标，即得点到的距离；（2）①先求点到的距离为，再根据三角形相似得的长度；②根据三角形面积公式求三个三角形面积，再用总面积相减得绿化区域面积，最后利用导数求函数最值

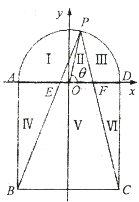
试题解析：以所在直线为轴，以线段的中垂线为轴建立平面直角坐标系.

（1）直线的方程为，

半圆的方程为 ，

由得.

所以，点到的距离为.

（2）①由题意，得.

直线的方程为

，

令，得

.

直线的方程为，

令，得 .

所以， 的长度为

， .

②区域Ⅳ、Ⅵ的面积之和为

，

区域Ⅱ的面积为

，

所以 .

设，则，

.

.

当且仅当，即时“”成立.

所以，休闲区域Ⅱ、Ⅳ、Ⅵ的面积的最小值为.

答：当时，绿化区域Ⅰ、Ⅲ、Ⅴ的面积之和最大.