题目内容
函数f（x）=2x3+3x-3的零点所在的区间为（ ）
| A、（-1，0） |
| B、（0，1） |
| C、（1，2） |
| D、（2，3） |
考点：函数零点的判定定理
专题：函数的性质及应用
分析：将f（-1），f（0），f（1）分别求出即可得出结论．
解答：
解：∵f（-1）=-2-3-3＜0，
f（0）=-3＜0，
f（1）=2+3-3=2＞0，
故f（x）=2x3+3x-3的零点所在的区间为（0，1），
故选：B．
f（0）=-3＜0，
f（1）=2+3-3=2＞0，
故f（x）=2x3+3x-3的零点所在的区间为（0，1），
故选：B．
点评：本题考察了函数的零点问题，是一道基础题．
练习册系列答案
相关题目
已知数列{an}的通项公式an=2014sin
，则a1+a2+…+a2014=（ ）
| nπ |
| 2 |
| A、2012 | B、2013 |
| C、2014 | D、2015 |
已知△ABC中，a=
，b=2，B=45°，则角A等于（ ）
| 6 |
| A、30° | B、90° |
| C、60° | D、60°或120° |
若正数a，b满足
+
=1，则
+
的最小值为（ ）
| 1 |
| a |
| 1 |
| b |
| 4 |
| a-1 |
| 16 |
| b-1 |
| A、16 | B、25 | C、36 | D、49 |
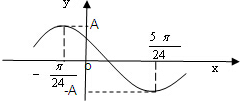已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π），其部分图象如图所示，且直线y=A与曲线y=f（x）（-
如图，平行四边形ABCD的对角线AC∩BD=0，且AB=BC=BD=6，BM=MC，将四边形ABCD沿对角线AC折起，得到三棱锥B-ACD，且DM=3