题目内容
设函数f(x)=lnx,g(x)=ax+1,a∈R,记F(x)=f(x)-g(x).
(Ⅰ)求曲线y=f(x)在x=e处的切线方程;
(Ⅱ)求函数F(x)的单调区间;
(Ⅲ)当a>0时,若函数F(x)没有零点,求a的取值范围.
(Ⅰ)求曲线y=f(x)在x=e处的切线方程;
(Ⅱ)求函数F(x)的单调区间;
(Ⅲ)当a>0时,若函数F(x)没有零点,求a的取值范围.
考点:利用导数研究函数的单调性,利用导数研究函数的极值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)求函数的导数,利用导数的几何意义,即可求曲线y=f(x)在x=e处的切线方程;
(Ⅱ)求函数F(x)的导数,利用函数导数和单调性之间的关系即可求函数的单调区间;
(Ⅲ)根据函数F(x)没有零点,转化为对应方程无解,即可得到结论.
(Ⅱ)求函数F(x)的导数,利用函数导数和单调性之间的关系即可求函数的单调区间;
(Ⅲ)根据函数F(x)没有零点,转化为对应方程无解,即可得到结论.
解答:
解:( I)f′(x)=
,则函数f(x)在x=e处的切线的斜率为k=
.
又f(e)=1,
所以函数f(x)在x=e处的切线方程为y-1=
(x-e),即y=
x.
(Ⅱ)F(x)=f(x)-g(x)=lnx-ax-1,F′(x)=
-a=
,(x>0).
①当a≤0时,F′(x)>0,F(x)在区间(0,+∞)上单调递增;
②当a>0时,令F′(x)<0,解得x>
;
令F′(x)>0,解得0<x<
.
综上所述,当a≤0时,函数F(x)的增区间是(0,+∞);
当a>0时,函数F(x)的增区间是(0,
),减区间是(
,+∞).
(Ⅲ)依题意,函数F(x)没有零点,
即F(x)=f(x)-g(x)=lnx-ax-1=0无解.
由(Ⅱ)知,当a>0时,函数F(x)在区间(0,
)上为增函数,区间(
,+∞)上为减函数,
由于F(1)=-a-1<0,只需F(
)=ln
-a•
-1=-lna-2<0,
解得a>e-2.
所以实数a的取值范围为(
,+∞).
| 1 |
| x |
| 1 |
| e |
又f(e)=1,
所以函数f(x)在x=e处的切线方程为y-1=
| 1 |
| e |
| 1 |
| e |
(Ⅱ)F(x)=f(x)-g(x)=lnx-ax-1,F′(x)=
| 1 |
| x |
| 1-ax |
| x |
①当a≤0时,F′(x)>0,F(x)在区间(0,+∞)上单调递增;
②当a>0时,令F′(x)<0,解得x>
| 1 |
| a |
令F′(x)>0,解得0<x<
| 1 |
| a |
综上所述,当a≤0时,函数F(x)的增区间是(0,+∞);
当a>0时,函数F(x)的增区间是(0,
| 1 |
| a |
| 1 |
| a |
(Ⅲ)依题意,函数F(x)没有零点,
即F(x)=f(x)-g(x)=lnx-ax-1=0无解.
由(Ⅱ)知,当a>0时,函数F(x)在区间(0,
| 1 |
| a |
| 1 |
| a |
由于F(1)=-a-1<0,只需F(
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
解得a>e-2.
所以实数a的取值范围为(
| 1 |
| e2 |
点评:本题主要考查导数的几何意义,以及函数的单调性和导数之间的关系,考查学生的运算能力.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
五名男生与两名女生排成一排照相,如果男生甲必须站在正中间,两名女生必须相邻,符合条件的排法共有( )
| A、48种 | B、192种 |
| C、240种 | D、288种 |
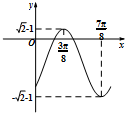 已知函数f(x)=asin(ωx+θ)-b的部分图象如图,其中ω>0,|θ|<
已知函数f(x)=asin(ωx+θ)-b的部分图象如图,其中ω>0,|θ|< 某同学用《几何画板》研究抛物线的性质:打开《几何画板》软件,绘制某抛物线E:y2=2px,在抛物线上任意画一个点S,度量点S的坐标(xS,yS),如图.
某同学用《几何画板》研究抛物线的性质:打开《几何画板》软件,绘制某抛物线E:y2=2px,在抛物线上任意画一个点S,度量点S的坐标(xS,yS),如图.