题目内容
在平面直角坐标系xoy中,以坐标原点O为极点,以x轴的正半轴为极轴建立极坐标系,得曲线C的极坐标方程为ρ=6cosθ(ρ>0),设A,B两点的极坐标依次分别为(2,-
)和(4,
).
(Ⅰ)求线段AB的长及曲线C的直角坐标方程;
(Ⅱ)设直线OA与曲线C的另一个交点为P,过点P作直线AB的垂线l,求直线l的方程.
| π |
| 4 |
| π |
| 4 |
(Ⅰ)求线段AB的长及曲线C的直角坐标方程;
(Ⅱ)设直线OA与曲线C的另一个交点为P,过点P作直线AB的垂线l,求直线l的方程.
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:(I)由A,B两点的极坐标依次分别为(2,-
)和(4,
).可得∠AOB=90°,利用勾股定理即可得出|AB|.
由曲线C的极坐标方程ρ=6cosθ(ρ>0)可得ρ2=6ρcosθ,利用极坐标与直角坐标的互化公式即可得出;
(II)利用极坐标与直角坐标的互化公式可得点A、B的直角坐标,可得直线AB的斜率,再利用相互垂直的直线斜率之间的关系可得l的斜率,把直线OA的方程与圆的方程联立可得点P的坐标,利用点斜式可得直线l的方程.
| π |
| 4 |
| π |
| 4 |
由曲线C的极坐标方程ρ=6cosθ(ρ>0)可得ρ2=6ρcosθ,利用极坐标与直角坐标的互化公式即可得出;
(II)利用极坐标与直角坐标的互化公式可得点A、B的直角坐标,可得直线AB的斜率,再利用相互垂直的直线斜率之间的关系可得l的斜率,把直线OA的方程与圆的方程联立可得点P的坐标,利用点斜式可得直线l的方程.
解答:
解:(I)由A,B两点的极坐标依次分别为(2,-
)和(4,
).
可得∠AOB=90°,∴|AB|=
=2
.
由曲线C的极坐标方程ρ=6cosθ(ρ>0)可得ρ2=6ρcosθ,∴x2+y2=6x,
化为(x-3)2+y2=9,可得圆心C(3,0),半径r=3.
(II)由A的极坐标(2,-
)化为直角坐标(2cos(-
),2sin(-
)),即(
,-
).
同理可得B(2
,2
).
∴直线OA的方程为:y=-x.
联立
解得
或
,得到P(3,-3).
∵kAB=
=3,l⊥AB,
∴kl=
=-
.
直线l的方程为y+3=-
(x-3),化为x+3y+6=0.
| π |
| 4 |
| π |
| 4 |
可得∠AOB=90°,∴|AB|=
| 22+42 |
| 5 |
由曲线C的极坐标方程ρ=6cosθ(ρ>0)可得ρ2=6ρcosθ,∴x2+y2=6x,
化为(x-3)2+y2=9,可得圆心C(3,0),半径r=3.
(II)由A的极坐标(2,-
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 2 |
| 2 |
同理可得B(2
| 2 |
| 2 |
∴直线OA的方程为:y=-x.
联立
|
|
|
∵kAB=
-
| ||||
|
∴kl=
| -1 |
| kAB |
| 1 |
| 3 |
直线l的方程为y+3=-
| 1 |
| 3 |
点评:本题考查了极坐标与直角坐标的互化公式、相互垂直的直线斜率之间的关系、直线与圆相交问题转化为方程联立可得交点的坐标直线的点斜式、勾股定理等基础知识与基本技能方法,考查了计算能力,属于中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 在平面直角坐标系xOy中,已知B(1,0),∠AOB=120°,|
在平面直角坐标系xOy中,已知B(1,0),∠AOB=120°,|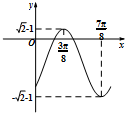 已知函数f(x)=asin(ωx+θ)-b的部分图象如图,其中ω>0,|θ|<
已知函数f(x)=asin(ωx+θ)-b的部分图象如图,其中ω>0,|θ|<