题目内容
8.已知向量$\overrightarrow{a}$=(x,1)与向量$\overrightarrow{b}$=(9,x)的夹角为π,则x=-3.分析 利用两个向量的夹角的定义,查两个向量共线的性质,求得x的值.
解答 解:∵向量$\overrightarrow{a}$=(x,1)与向量$\overrightarrow{b}$=(9,x)的夹角为π,
则(9,x)=-λ•(x,1),λ>0,
∴9=-λx,x=-λ,求得x=-3,
故答案为:-3.
点评 本题主要考查两个向量的夹角的定义,查两个向量共线的性质,属于基础题.

练习册系列答案
相关题目
19.已知抛物线C1:y2=ax(a>0)的焦点与双曲线C2:$\frac{x^2}{4}-\frac{y^2}{b^2}=1({b>0})$的右焦点重合,记为F点,点M与点P(4,6)分别为曲线C1,C2上的点,则|MP|+|MF|的最小值为( )
| A. | $\frac{5}{2}$ | B. | 8 | C. | $\frac{13}{2}$ | D. | $\frac{11}{2}$ |
3.已知复数z满足(1+i)z=|$\sqrt{3}$+i|,i为虚数单位,则z等于( )
| A. | 1-i | B. | 1+i | C. | $\frac{1}{2}$-$\frac{1}{2}$i | D. | $\frac{1}{2}$+$\frac{1}{2}$i |
18.已知A(-2,0),B(2,0),斜率为k的直线l上存在不同的两点M,N满足:|MA|-|MB|=2$\sqrt{3}$,|NA|-|NB|=2$\sqrt{3}$,且线段MN的中点为(6,1),则k的值为( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
19.春天来了,某学校组织学生外出踏青.4位男生和3位女生站成一排合影留念,男生甲和乙要求站在一起,3位女生不全站在一起,则不同的站法种数是( )
| A. | 964 | B. | 1080 | C. | 1152 | D. | 1296 |
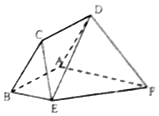 如图,已知菱形ABCD与直角梯形ABEF所在的平面互相垂直,其中BE∥AF,AB⊥AF,AB=BE=$\frac{1}{2}$AF=2,∠CBA=$\frac{π}{3}$.
如图,已知菱形ABCD与直角梯形ABEF所在的平面互相垂直,其中BE∥AF,AB⊥AF,AB=BE=$\frac{1}{2}$AF=2,∠CBA=$\frac{π}{3}$.