题目内容
19.春天来了,某学校组织学生外出踏青.4位男生和3位女生站成一排合影留念,男生甲和乙要求站在一起,3位女生不全站在一起,则不同的站法种数是( )| A. | 964 | B. | 1080 | C. | 1152 | D. | 1296 |
分析 根据题意,先用捆绑法分析“甲和乙站在一起”的情况数目,再其中求出“甲和乙站在一起且女生全站在一起”的情况数目,用“甲和乙站在一起”的情况数目减去“甲和乙站在一起且女生全站在一起”的情况数目即可得答案.
解答 解:根据题意,男生甲和乙要求站在一起,将2人看成一个整体,考虑2人的顺序,有A22种情况,
将这个整体与其余5人全排列,有A66种情况,
则甲和乙站在一起共有A22A66=1440种站法,
其中男生甲和乙要求站在一起且女生全站在一起有A22A33A44=288种;
则符合题意的站法共有1440-288=1152种;
故选:C.
点评 本题考查排列、组合的应用,运用排除法进行分析,注意掌握常见问题的处理方法.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
7.集合$M=\left\{{\left.x\right|x=\frac{n}{2}+1,n∈Z}\right\}$,$N=\left\{{\left.y\right|y=m+\frac{1}{2},m∈Z}\right\}$,则两集合M,N的关系为( )
| A. | M∩N=∅ | B. | M=N | C. | M?N | D. | N?M |
8.已知函数f(x)=a-x2(1≤x≤2)与g(x)=x+2的图象上存在关于x轴对称的点,则实数a的取值范围是( )
| A. | [-2,0] | B. | [-$\frac{9}{4}$,0] | C. | [2,4] | D. | [-$\frac{9}{4}$,+∞) |
9.已知集合$M=\left\{{x\left|{\frac{x-2}{x-3}<0}\right.}\right\},N=\left\{{x\left|{{{log}_{\frac{1}{2}}}(x-2)≥1}\right.}\right\}$,则M∩N=( )
| A. | $[{\frac{5}{2},3})$ | B. | $({2,\frac{5}{2}}]$ | C. | $[{2,\frac{5}{2}}]$ | D. | $({\frac{5}{2},3})$ |
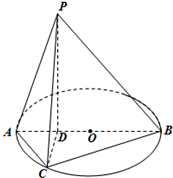 如图,已知PD垂直于以AB为直径的圆O所在的平面,点D在线段AB上,点C为圆O上一点,且BD=PD=3,AC=2AD=2.
如图,已知PD垂直于以AB为直径的圆O所在的平面,点D在线段AB上,点C为圆O上一点,且BD=PD=3,AC=2AD=2.