题目内容
16.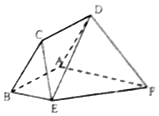 如图,已知菱形ABCD与直角梯形ABEF所在的平面互相垂直,其中BE∥AF,AB⊥AF,AB=BE=$\frac{1}{2}$AF=2,∠CBA=$\frac{π}{3}$.
如图,已知菱形ABCD与直角梯形ABEF所在的平面互相垂直,其中BE∥AF,AB⊥AF,AB=BE=$\frac{1}{2}$AF=2,∠CBA=$\frac{π}{3}$.(Ⅰ)求证:AF⊥BC;
(Ⅱ)线段AB上是否存在一点G,使得直线FG与平面DEF所成的角的正弦值为$\frac{\sqrt{93}}{31}$,若存在,求AG的长;若不存在,说明理由.
分析 (Ⅰ)利用面面垂直的性质,证明AF⊥平面ABCD,即可证明:AF⊥BC;
(Ⅱ)建立如图所示的坐标系,求出平面DEF的法向量,利用直线FG与平面DEF所成的角的正弦值为$\frac{\sqrt{93}}{31}$,可得结论.
解答 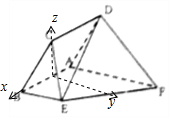 (Ⅰ)证明:∵菱形ABCD与直角梯形ABEF所在的平面互相垂直,AB⊥AF,
(Ⅰ)证明:∵菱形ABCD与直角梯形ABEF所在的平面互相垂直,AB⊥AF,
∴AF⊥平面ABCD,
∵BC?平面ABCD,AF⊥BC;
(Ⅱ)解:取AB的中点O,连接CO,则CO⊥AB,
∵菱形ABCD与直角梯形ABEF所在的平面互相垂直,
∴CO⊥平面ABEF,
作OM∥AF,建立如图所示的坐标系,则D(-2,0,$\sqrt{3}$),F(-1,4,0),E(1,2,0),
∴$\overrightarrow{DF}$=(1,4,-$\sqrt{3}$),$\overrightarrow{EF}$=(-2,2,0),
设平面DEF的法向量为$\overrightarrow{m}$=(x,y,z),则$\left\{\begin{array}{l}{x+4y-\sqrt{3}z=0}\\{-2x+2y=0}\end{array}\right.$,取$\overrightarrow{m}$=(1,1,$\frac{5}{\sqrt{3}}$),
设G(λ,0,0),λ∈[-1,1],则$\overrightarrow{GF}$=(-λ-1,4,0)
∵直线FG与平面DEF所成的角的正弦值为$\frac{\sqrt{93}}{31}$,
∴$\frac{|-λ-1+4|}{\sqrt{(λ+1)^{2}+16}×\sqrt{\frac{31}{3}}}$=$\frac{\sqrt{93}}{31}$,
∴λ=-1∈[-1,1],
∴AG=0,直线FG与平面DEF所成的角的正弦值为$\frac{\sqrt{93}}{31}$.
点评 本题考查了空间中垂直关系的判断与应用问题,也考查了用向量法求线面角,考查了空间想象能力与逻辑思维能力,是综合性问题.

 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
| A. | -i | B. | i | C. | 1+i | D. | 1-i |
| A. | (3,8) | B. | (2,16) | C. | (4,8) | D. | $(2\sqrt{2},16)$ |
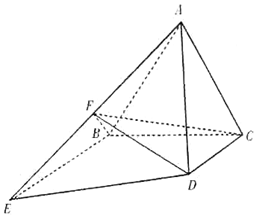 如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AB的中点.
如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AB的中点.