题目内容
1．已x，y∈R，满足x2+y2+2x=0，则2x+y的最大值、最小值分别为-2+$\sqrt{5}$，-2-$\sqrt{5}$．分析 利用直线与圆相切的充要条件即可得出．
解答 解：∵实数x，y满足x2+y2+2x=0，配方为：（x+1）2+y2=1，圆心为C（-1，0），半径为r=1．
令2x+y=t，则$\frac{|-2-t|}{\sqrt{5}}$≤1，化为：-2-$\sqrt{5}$≤t≤-2+$\sqrt{5}$，当且仅当直线x+y=t与圆相切时取等号．
则2x+y的最大值、最小值分别为-2+$\sqrt{5}$，-2-$\sqrt{5}$，
故答案为：-2+$\sqrt{5}$，-2-$\sqrt{5}$．
点评 本题考查了直线与圆的位置关系、点到直线的距离公式公式、不等式的解法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
11．若z=（a-1）+ai为纯虚数，其中a∈R，则$\frac{a+{i}^{7}}{1+ai}$=（ ）
| A． | -i | B． | i | C． | 1+i | D． | 1-i |
13．若将函数y=3cos（2x+$\frac{π}{2}$）的图象向右平移$\frac{π}{6}$个单位长度，则平移后图象的一个对称中心是（ ）
| A． | （$\frac{π}{6}$，0） | B． | （-$\frac{π}{6}$，0） | C． | （$\frac{π}{12}$，0） | D． | （-$\frac{π}{12}$，0） |
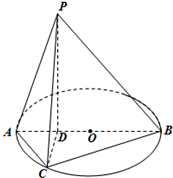如图，已知PD垂直于以AB为直径的圆O所在的平面，点D在线段AB上，点C为圆O上一点，且BD=PD=3，AC=2AD=2．