题目内容
13.在极坐标系中,点A($\sqrt{3}$,$\frac{π}{6}$)、B($\sqrt{3}$,$\frac{π}{2}$),直线l平行于直线AB,且将封闭曲线C:ρ=2cos(θ-$\frac{π}{3}$)(ρ≥0)所围成的面积平分,以极点为坐标原点,极轴为x轴正半轴建立直角坐标系(Ⅰ)在直角坐标系中,求曲线C及直线l的参数方程;
(Ⅱ)设点M为曲线C上的动点,求|MA|2+|MB|2的取值范围.
分析 (I)曲线C:ρ=2cos(θ-$\frac{π}{3}$)(ρ≥0)即ρ2=2ρ($\frac{1}{2}$cosθ+$\frac{\sqrt{3}}{2}$sinθ),利用互化公式可得直角坐标方程.点A($\sqrt{3}$,$\frac{π}{6}$)、B($\sqrt{3}$,$\frac{π}{2}$),利用互化公式可得直角坐标,可得kAB.根据直线l平行于直线AB,将封闭曲线C:ρ=2cos(θ-$\frac{π}{3}$)(ρ≥0)所围成的面积平分,可得直线l的斜率kl=kAB,经过圆心C.可得直线l的参数方程..
(II)设M$(\frac{1}{2}+cosθ,\frac{\sqrt{3}}{2}+sinθ)$,利用两点之间的距离公式可得|MA|2+|MB|2=4-2$sin(θ+\frac{π}{6})$及其范围.
解答 解:(I)曲线C:ρ=2cos(θ-$\frac{π}{3}$)(ρ≥0)即ρ2=2ρ($\frac{1}{2}$cosθ+$\frac{\sqrt{3}}{2}$sinθ),化为直角坐标方程:x2+y2=x+$\sqrt{3}$y.
配方为:$(x-\frac{1}{2})^{2}$+$(y-\frac{\sqrt{3}}{2})^{2}$=1.
点A($\sqrt{3}$,$\frac{π}{6}$)、B($\sqrt{3}$,$\frac{π}{2}$),分别化为直角坐标:A$(\frac{3}{2},\frac{\sqrt{3}}{2})$,B$(0,\sqrt{3})$,kAB=$\frac{\frac{\sqrt{3}}{2}-\sqrt{3}}{\frac{3}{2}-0}$=-$\frac{\sqrt{3}}{3}$.
∵直线l平行于直线AB,将封闭曲线C所围成的面积平分,
∴直线的斜率kl=-$\frac{\sqrt{3}}{3}$,经过圆心C$(\frac{1}{2},\frac{\sqrt{3}}{2})$.
∴直线l的参数方程为:$\left\{\begin{array}{l}{x=\frac{1}{2}-\frac{\sqrt{3}}{2}t}\\{y=\frac{\sqrt{3}}{2}+\frac{1}{2}t}\end{array}\right.$(t为参数).
(II)设M$(\frac{1}{2}+cosθ,\frac{\sqrt{3}}{2}+sinθ)$,则|MA|2+|MB|2=(cosθ-1)2+sin2θ+$(\frac{1}{2}+cosθ)^{2}$+$(sinθ-\frac{\sqrt{3}}{2})^{2}$
=4-$\sqrt{3}$sinθ-cosθ
=4-2$sin(θ+\frac{π}{6})$∈[2,6].
点评 本题考查了参数方程、极坐标方程化为直角坐标方程、圆的性质、平行线的斜率之间的关系,考查了推理能力与计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $-\frac{7}{2}$ | B. | $\frac{9}{2}$ | C. | $\frac{7}{2}$ | D. | $-\frac{9}{2}$ |
| A. | (3,8) | B. | (2,16) | C. | (4,8) | D. | $(2\sqrt{2},16)$ |
| A. | -2$\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | 0 | D. | 2$\sqrt{2}$ |
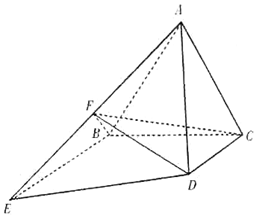 如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AB的中点.
如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AB的中点.