题目内容
1．若函数f（x）=$\frac{x}{ax+b}$（a≠0），f（2）=1，又方程f（x）=x有唯一解，则a+b=$\frac{3}{2}$．分析 易知f（2）=$\frac{2}{2a+b}$=1，化简f（x）-x=$\frac{x（1-ax-b）}{ax+b}$，从而可得$\left\{\begin{array}{l}{2a+b=2}\\{1-b=0}\end{array}\right.$，从而解得．
解答 解：由题意得，
f（2）=$\frac{2}{2a+b}$=1，
f（x）-x=$\frac{x}{ax+b}$-x=$\frac{x（1-ax-b）}{ax+b}$=0，
故$\left\{\begin{array}{l}{2a+b=2}\\{1-b=0}\end{array}\right.$，
解得，a=$\frac{1}{2}$，b=1；
故a+b=$\frac{3}{2}$；
故答案为：$\frac{3}{2}$．
点评 本题考查了函数的化简与运算，属于中档题．
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
11．已知某几何体的三视图如图所示，则该几何体的表面积（ ）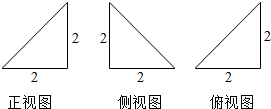
| A． | 6 | B． | $6+2\sqrt{3}$ | C． | $8+8\sqrt{2}$ | D． | $4+4\sqrt{2}$ |
9．
每年七夕，琳琅满目的饰品在各大品牌店中成为年轻人亲眯的对象，这也使各大珠宝公司挖空心思，设计出匠心独运的饰品．某珠宝公司市场专员甲对该公司的一款项链的单价x（百元）和单位时间内的销售量y（件）之间的关系作出价格分析，所得数据如下：
其中价格x（元）恰为公差为2的等差数列{an}的前5项，且等差数列{an}的前10项和为230．
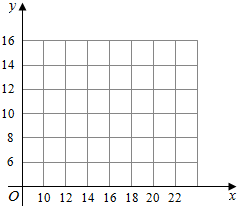
（1）请根据上述数据在下列网格纸中绘制散点图；
（2）请根据表格数据计算项链的单价x（百元）和单位时间内的销售量y（件）之间的回归直线方程．
$\left\{\begin{array}{l}{\stackrel{∧}{b}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}=\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}}\\{\stackrel{∧}{a}=\overline{y}-\stackrel{∧}{b}\overline{x}}\end{array}\right.$．
每年七夕，琳琅满目的饰品在各大品牌店中成为年轻人亲眯的对象，这也使各大珠宝公司挖空心思，设计出匠心独运的饰品．某珠宝公司市场专员甲对该公司的一款项链的单价x（百元）和单位时间内的销售量y（件）之间的关系作出价格分析，所得数据如下：| 单价x（百元） | a1 | a2 | a3 | a4 | a5 |
| 单位时间内销售量y（件） | 14 | 13 | 10 | 7 | 5 |
（1）请根据上述数据在下列网格纸中绘制散点图；
（2）请根据表格数据计算项链的单价x（百元）和单位时间内的销售量y（件）之间的回归直线方程．
$\left\{\begin{array}{l}{\stackrel{∧}{b}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}=\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}}\\{\stackrel{∧}{a}=\overline{y}-\stackrel{∧}{b}\overline{x}}\end{array}\right.$．
16．已知函数f（x）=（sinx-cosx）sinx，x∈R，则f（x）的最小正周期是（ ）
| A． | π | B． | 2π | C． | $\frac{π}{2}$ | D． | 2 |
13．Sn表示数列{an}（n≥1）的前n项和，已知a1=1，且?n≥1，Sn+1=4an+2，则a2013等于（ ）
| A． | 3019•22012 | B． | 3019•22013 | C． | 3018•22012 | D． | 以上答案均不对 |