题目内容
10．集合M={x|lg（1-x）＜1}，N={x|-1≤x≤1}，则M∩N=（ ）| A． | （-9，1） | B． | （-9，1] | C． | [-1，1] | D． | [-1，1） |
分析 先分别求出集合M，N，由此利用交集定义能求出M∩N．
解答 解：∵集合M={x|lg（1-x）＜1}=x|-9＜x＜1}，
N={x|-1≤x≤1}，
∴M∩N={x|-1≤x＜1}=[-1，1）．
故选：D．
点评 本题考查交集的求法，是基础题，解题时要认真审题，注意交集定义的合理运用．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
20．下列说法中正确的是（ ）
| A． | 经过不同的三点有且只有一个平面 | |
| B． | 没有公共点的两条直线一定平行 | |
| C． | 垂直于同一平面的两直线是平行直线 | |
| D． | 垂直于同一平面的两平面是平行平面 |
15．如图，扇形的半径为1，圆心角∠BAC=150°，点P在弧BC上运动，$\overrightarrow{AP}=m\overrightarrow{AB}+n\overrightarrow{AC}$，则$\sqrt{3}m-n$的最大值是（ ）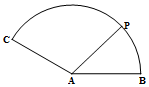
| A． | 1 | B． | $\sqrt{3}$ | C． | 2 | D． | $2\sqrt{3}$ |
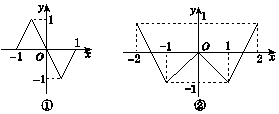已知奇函数f（x）、偶函数g（x）的图象分别如图①②所示，若方程f[g（x）]=0，g[f（x）]=0的实根个数分别为a，b，则a+b等于（ ）