题目内容
10.若a+1,2a+2,3a+5成等比数列,则实数a的值为1.分析 由等比数列可得(2a+2)2=(a+1)(3a+5),解方程验证可得.
解答 解:∵a+1,2a+2,3a+5成等比数列,
∴(2a+2)2=(a+1)(3a+5),
整理可得(a+1)(a-1)=0,
解得a=-1或a=1,
当a=-1时,a+1=2a+2=0,不满足等比数列.
故答案为:1
点评 本题考查等比数列的通项公式,属基础题.

练习册系列答案
相关题目
2.在△ABC中,a=2$\sqrt{3},b=3\sqrt{2},cosC=\frac{1}{3}$,则△ABC的面积为( )
| A. | 3$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | $\sqrt{3}$ |
19.已知i为虚数单位,若复数z满足z=i•(2015+2016i),则$\overline z$为( )
| A. | 2015+2016i | B. | 2015-2016i | C. | -2016+2015i | D. | -2016-2015i |
20.已知点(a,3)和点(3,a)在直线x-2y=0的两侧,则a的取值范围是( )
| A. | ($\frac{3}{2}$,6) | B. | (-6,$\frac{3}{2}$) | C. | (-∞,-6)∪($\frac{3}{2}$,+∞) | D. | (-∞,$\frac{3}{2}$)∪(6,+∞) |
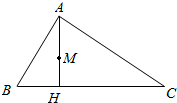 如图,在△ABC中,AB=2,BC=3,∠ABC=60°,AH⊥BC于点H,M为AH的中点,若$\overrightarrow{AM}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{BC}$,则λ+μ=$\frac{2}{3}$.
如图,在△ABC中,AB=2,BC=3,∠ABC=60°,AH⊥BC于点H,M为AH的中点,若$\overrightarrow{AM}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{BC}$,则λ+μ=$\frac{2}{3}$.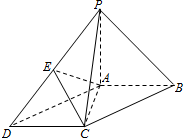 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且AB=AC=$\frac{1}{2}$PA=1,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且AB=AC=$\frac{1}{2}$PA=1,点E是PD的中点.