题目内容
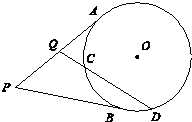如图，p为⊙O外一点，过P点作⊙O的两条切线，切点分别为A，B，过PA的中点Q作割线交⊙O于C，D两点，若QC=1，CD=4，则PB=考点：与圆有关的比例线段,圆的切线的性质定理的证明
专题：直线与圆
分析：由已知条件利用切割线定理得AQ2=CQ•DQ=1×（1+4）=5，由此能求出PB=PA=2AQ=2
．
| 5 |
解答：
解：∵p为⊙O外一点，过P点作⊙O的两条切线，切点分别为A，B，
过PA的中点Q作割线交⊙O于C，D两点，QC=1，CD=4，
∴AQ2=CQ•DQ=1×（1+4）=5，
∴AQ=
，
∴PB=PA=2AQ=2
．
故答案为：2
．
过PA的中点Q作割线交⊙O于C，D两点，QC=1，CD=4，
∴AQ2=CQ•DQ=1×（1+4）=5，
∴AQ=
| 5 |
∴PB=PA=2AQ=2
| 5 |
故答案为：2
| 5 |
点评：本题考查线段长的求法，是中档题，解题时要认真审题，注意切割线定理的合理运用．
练习册系列答案
云南师大附小一线名师提优作业系列答案
相关题目
已知（1+x）8=a0+a1x+a2x2+…+a8x8，则a1+a2+…+a8的值是（ ）
| A、28 |
| B、28-1 |
| C、26-1 |
| D、26 |
设直线过点（0，a），其斜率为1，且与圆x2+y2=4相切，则a的值为（ ）
| A、±4 | ||
B、±2
| ||
| C、4x+2y=5 | ||
| D、4x-2y=5 |