题目内容
3.已知cos(α+β)=1,求证:sin(α+2β)=sinβ.分析 利用同角三角函数的基本关系求得sin(α+β)=0,再根据sin(α+2β)=sin[(α+β)+β],利用两角而和的正弦公式,证得等式成立.
解答 证明:∵cos(α+β)=1,∴sin(α+β)=0,
∴sin(α+2β)=sin[(α+β)+β]=sin(α+β)cosβ+cos(α+β)sinβ=0+1•sinβ=sinβ,
∴sin(α+2β)=sinβ成立.
点评 本题主要考查同角三角函数的基本关系、两角而和的正弦公式的应用,属于基础题.

练习册系列答案
相关题目
16.如图所示的程序框图中,输出的S的值是( )
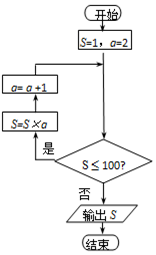

| A. | 80 | B. | 100 | C. | 120 | D. | 140 |
18. 如图,在边长为a的正方形内有不规则图形Ω.向正方形内随机撒豆子,若撒在图形Ω内和正方形内的豆子数分别为57,100,则图形Ω面积的估计值为( )
如图,在边长为a的正方形内有不规则图形Ω.向正方形内随机撒豆子,若撒在图形Ω内和正方形内的豆子数分别为57,100,则图形Ω面积的估计值为( )
 如图,在边长为a的正方形内有不规则图形Ω.向正方形内随机撒豆子,若撒在图形Ω内和正方形内的豆子数分别为57,100,则图形Ω面积的估计值为( )
如图,在边长为a的正方形内有不规则图形Ω.向正方形内随机撒豆子,若撒在图形Ω内和正方形内的豆子数分别为57,100,则图形Ω面积的估计值为( )| A. | $\frac{57a}{100}$ | B. | $\frac{100a}{57}$ | C. | $\frac{57{a}^{2}}{100}$ | D. | $\frac{100{a}^{2}}{57}$ |