题目内容

15．抛物线x2+y=0的焦点坐标为（0，-$\frac{1}{4}$）．

分析 先把抛物线的方程化为标准形式，再利用抛物线 x2=-2py 的焦点坐标为（0，-$\frac{p}{2}$），求出抛物线x2+y=0的焦点坐标．

解答 解：∵抛物线x2+y=0，即x2=-y，∴p=$\frac{1}{2}$，$\frac{p}{2}$=$\frac{1}{4}$，
∴焦点坐标是 （0，-$\frac{1}{4}$），
故答案为：（0，-$\frac{1}{4}$）．

点评 本题考查抛物线的标准方程和简单性质的应用，抛物线 x2=-2py 的焦点坐标为（0，-$\frac{p}{2}$）．

练习册系列答案
相关题目
7．已知圆C1：x2+y2=r2（r＞0）与抛物线C2：x2=2py（p＞0），点（$\sqrt{2}$，-2）是圆C1与抛物线C2准线l的一个交点．
（1）求圆C1与抛物线C2的方程；
（2）若点M是直线l上的动点，过点M作抛物线C2的两条切线，切点分别为A、B，直线AB与圆C1交于点E、F，求$\overrightarrow{OE}$•$\overrightarrow{OF}$的取值范围．
6．一个均匀小正方体的6个面中，三个面上标以数字0，两个面上标以数字1，一个面上标以数字2，将这个小正方体抛掷1次，则向上的数字为2的概率为$\frac{1}{6}$；将这个小正方体抛掷2次，则向上的数字之积的数学期望是$\frac{4}{9}$．
3．已知cos（α+β）=1，求证：sin（α+2β）=sinβ．
10．已知函数y=f（x+1）的图象关于y轴对称，且函数f（x）在（1，+∞）上单调，若数列{an}是公差不为0的等差数列，且f（a6）=f（a20），则{an}的前25项之和为（　　）
A．0B．$\frac{25}{2}$C．25D．50
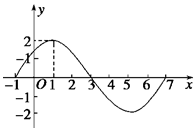20．已知函数f（x）=Asin（ωx+φ） （A＞0，ω＞0，|φ|＜$\frac{π}{2}$，x∈R）的图象的一部分如图所示．
（1）求函数f（x）的解析式．
（2）若f（$\frac{4α}{π}$）=1且α∈（$\frac{π}{4}$，$\frac{3π}{4}$），求sinα．
7．已知直线y=ax-2与直线y=（a+2）x-2互相垂直，则a=（　　）
A．-1B．0C．1D．2
4．已知$tanα=\frac{1}{2}$，则sin2α的值为$\frac{4}{5}$．
5．某商店将进价每个10元的商品按每个18元售出时，每天可卖出60个，商店经理到市场上做了一番调查后发现，若将这种商品的售价（在每个18元的基础上）每提高1元，则日销售量就减少5个；若将这种商品的售价（在每个18元的基础上）每降低1元，则日销售量增加10个．为了每日获得最大利润，则商品的售价应定为（　　）
A．10元B．15元C．20元D．25元

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网