题目内容
已知函数y=f(x)是定义在R上的偶函数,且f(1)=0,当x∈(-∞,0)时,xf′(x)<-f(-x)(其中f′(x)是f(x)的导函数),则不等式xf(x)>0的解集为( )
| A、(-∞,-1)∪(0,1) |
| B、(-∞,-1)∪(1,+∞) |
| C、(-1,0)∪(0,1) |
| D、(-1,0)∪(1,+∞) |
考点:导数的运算,函数奇偶性的性质,其他不等式的解法
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:由f(x)为偶函数得到f(-x)=f(x),有xf′(x)+f(x)<0,由导数的积的运算得到[xf(x)]′<0,令F(x)=xf(x),则F(x)为奇函数,且在(-∞,0)上是减函数,在(0,+∞)上是减函数,由f(1)=0,F(1)=F(-1)=0,不等式xf(x)>0等价为F(x)>0,分
或
,由F(x)的单调性即可得到原不等式的解集.
|
|
解答:
解:∵函数y=f(x)是定义在R上的偶函数,
∴f(-x)=f(x),
∴当x∈(-∞,0)时,xf′(x)<-f(-x),即xf′(x)+f(x)<0,
∴[xf(x)]′<0,
∴令F(x)=xf(x),则F(x)为奇函数,且在(-∞,0)上是减函数,在(0,+∞)上是减函数,
∵f(1)=0,且f(-1)=0
∴F(1)=F(-1)=0,
∴不等式xf(x)>0等价为F(x)>0,
∴
或
∴
或
即x∈(-∞,-1)∪(0,1),
∴原不等式的解集为:(-∞,-1)∪(0,1),
故选A.
∴f(-x)=f(x),
∴当x∈(-∞,0)时,xf′(x)<-f(-x),即xf′(x)+f(x)<0,
∴[xf(x)]′<0,
∴令F(x)=xf(x),则F(x)为奇函数,且在(-∞,0)上是减函数,在(0,+∞)上是减函数,
∵f(1)=0,且f(-1)=0
∴F(1)=F(-1)=0,
∴不等式xf(x)>0等价为F(x)>0,
∴
|
|
∴
|
|
∴原不等式的解集为:(-∞,-1)∪(0,1),
故选A.
点评:本题主要考查函数的性质及应用,考查奇偶函数的定义及应用,函数的单调性及应用,以及应用导数的运算法则构造函数的能力,同时考查解不等式的运算能力,是函数的综合题.

练习册系列答案
相关题目
已知m,n是不同直线,α是平面,m?α,则“n∥m”是“n∥α”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
复数
等于( )
| 3-2i |
| 2i |
A、-1+
| ||
B、1-
| ||
C、-1-
| ||
D、1+
|
已知a=sin
sin
,b=cos2
,c=cos
-sin
,则( )
| π |
| 8 |
| 5π |
| 8 |
| π |
| 12 |
| π |
| 12 |
| π |
| 12 |
| A、a<c<b |
| B、a<b<c |
| C、b<a<c |
| D、c<a<b |
已知等差数列{an}的前n项和为Sn(n∈N*),且an=2n+λ,若数列{Sn}在{n|n≥5,n∈N+}内为递增数列,则实数λ的取值范围为( )
| A、(-3,+∞) |
| B、(-10,+∞) |
| C、[-11,+∞) |
| D、(-12,+∞) |
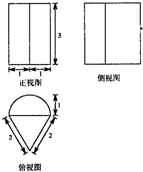
某几何体的三视图如图所示,则该几何体的体积等于( )

A、
| ||||
B、3(
| ||||
C、3(
| ||||
D、
|
若函数f(x)=cos2x-
(x∈R),则f(x)是( )
| 1 |
| 2 |
A、最小正周期为
| ||
| B、最小正周期为π的奇函数 | ||
| C、最小正周期为2π的偶函数 | ||
| D、最小正周期为π的偶函数 |