题目内容
设a、b∈R，集合{a，b}={0，a2}，则b-a= ．
考点：集合的相等
专题：集合
分析：由集合{a，b}={0，a2}，可得：a=0，b=a2，或b=0，a=a2，结合集合元素的互异性分类讨论，可得答案．
解答：
解：∵集合{a，b}={0，a2}，
∴a=0，b=a2，或b=0，a=a2，
当a=0，b=a2时，a=b=0，这与集合元素的互异性矛盾，
当b=0，a=a2时，解得a=0，此时与集合元素的互异性矛盾，舍去，或a=1，
综上所述，a=1，b=0，
故b-a=-1，
故答案为：-1
∴a=0，b=a2，或b=0，a=a2，
当a=0，b=a2时，a=b=0，这与集合元素的互异性矛盾，
当b=0，a=a2时，解得a=0，此时与集合元素的互异性矛盾，舍去，或a=1，
综上所述，a=1，b=0，
故b-a=-1，
故答案为：-1
点评：本题考查集合元素的特征与集合相等的含义，注意从特殊元素下手，有利于找到解题切入点．
练习册系列答案
相关题目
已知定义在R上的函数f（x）满足f（x）•f（x+
π）=-1．若f（
）=2，则f（11π）等于（ ）
| 3 |
| 2 |
| π |
| 2 |
| A、-2 | ||
B、-
| ||
C、
| ||
| D、2 |
若函数f（x）=ax2-ln（2x+1）在区间[1，2]上为单调函数，则实数a不可能取到的值为（ ）
| A、1 | ||
B、
| ||
C、
| ||
D、
|
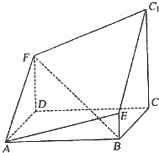如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的，其中AB=4，BC=2，CC1=3，BE=1