题目内容
若将6本不同书放到5个不同盒子里，有多少种不同放法（ ）
A、
| ||
B、
| ||
| C、56 | ||
| D、65 |
考点：分步乘法计数原理
专题：计算题,排列组合
分析：将6本不同书放到5个不同盒子里，每本书都有5种放法，根据乘法原理可得结论．
解答：
解：将6本不同书放到5个不同盒子里，每本书都有5种放法，
根据乘法原理可得不同放法为56种．
故选：C．
根据乘法原理可得不同放法为56种．
故选：C．
点评：本题考查分步乘法计数原理，考查学生的计算能力，比较基础．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
将5名大学毕业生全部分配给3所不同的学校，不同的分配方式的种数有（ ）
| A、8 | B、15 | C、125 | D、243 |
若等差数列{an}满足：
＜-1，且其前n项和Sn有最大值．则当数列Sn＞0时，n的值为（ ）
| a11 |
| a12 |
| A、20 | B、21 | C、23 | D、22 |
下列命题中：
①
∥
?存在唯一的实数λ∈R，使得
=λ
②|
•
|≤|
|•|
|
③（
•
）•
=
•（
•
）
④
与
共线，
与
共线，则
与
共线
⑤若
•
=
•
且
≠0，则
=
，
其中正确命题序号是（ ）
①
| a |
| b |
| b |
| a |
②|
| a |
| b |
| a |
| b |
③（
| a |
| b |
| c |
| a |
| b |
| c |
④
| a |
| b |
| b |
| c |
| a |
| c |
⑤若
| a |
| b |
| b |
| c |
| b |
| a |
| c |
其中正确命题序号是（ ）
| A、①②⑤ | B、② | C、②⑤ | D、①④⑤ |
设f（x）=ax+a+4，若f′（1）=2，则a等于（ ）
| A、1 | B、-2 | C、2 | D、-3 |
收集一只棉铃虫的产卵数y与温度X的几组数据后发现两个变量有相关关系，并按不同的曲线来拟合y与X之间的回归方程，算出对应相关指数R2如下表：
则这组数据模型的回归方程的最好选择应是（ ）
则这组数据模型的回归方程的最好选择应是（ ）
| 拟合曲线 | 直 线 | 指数曲线 | 抛 物 线 | 二次曲线 | ||||||||||
| y与x回归方程 |
|
|
|
| ||||||||||
| 相关指数R2 | 0.746 | 0.996 | 0.902 | 0.002 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
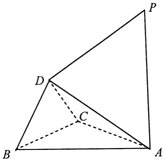已知△ABC与△DBC都是边长为2的等边三角形，且平面ABC⊥平面DBC，过点A作PA⊥平面ABC，且AP=2