题目内容
下列函数是奇函数的是( )
| A、f(x)=-|x| |
| B、f(x)=2x+2-x |
| C、f(x)=lg(1+x)-lg(1-x) |
| D、f(x)=x3-1 |
考点:函数奇偶性的判断
专题:函数的性质及应用
分析:根据函数奇偶性的定义即可得到结论.
解答:
解:f(-x)=-|-x|=-|x|=f(x),故A是偶函数.
f(-x)=2x+2-x=f(x),故B是偶函数.
f(-x)=lg(1-x)-lg(1+x)=-[lg(1+x)-lg(1-x)]=-f(x),故C是奇函数.
f(-x)=-x3-1≠-f(x),故D不是奇函数.
故选:C
f(-x)=2x+2-x=f(x),故B是偶函数.
f(-x)=lg(1-x)-lg(1+x)=-[lg(1+x)-lg(1-x)]=-f(x),故C是奇函数.
f(-x)=-x3-1≠-f(x),故D不是奇函数.
故选:C
点评:本题主要考查函数奇偶性的判断,根据函数奇偶性的定义是解决本题的关键.

练习册系列答案
相关题目
已知正四面体A-BCD棱长都为
,M为AC中点,N为CD中点,求异面直线BM与AN所成角的余弦值( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
等差数列{an}共有20项,其中奇数项的和为15,偶数项的和为45,则该数列的公差为( )
| A、-3 | B、3 | C、-2 | D、-1 |
设f(x)=ax+a+4,若f′(1)=2,则a等于( )
| A、1 | B、-2 | C、2 | D、-3 |
已知椭圆
+
=1,则以点M(-1,1)为中点的弦所在直线方程为( )
| x2 |
| 4 |
| y2 |
| 3 |
| A、3x-4y+7=0 |
| B、3x+4y-1=0 |
| C、4x-3y+7=0 |
| D、4x+3y+1=0 |
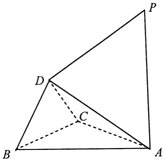 已知△ABC与△DBC都是边长为2的等边三角形,且平面ABC⊥平面DBC,过点A作PA⊥平面ABC,且AP=2
已知△ABC与△DBC都是边长为2的等边三角形,且平面ABC⊥平面DBC,过点A作PA⊥平面ABC,且AP=2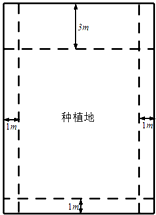 某部队驻扎在青藏高原上,那里海拔高、寒冷缺氧、四季风沙、没有新鲜蔬菜,生活条件极为艰苦.但战士们不计个人得失,扎根风雪高原,以钢铁般的意志,自力更生,克服恶劣的自然环境.该部队现计划建造一个室内面积为800m2的矩形蔬菜温室,在温室内,与左、右两侧及后侧的内墙各保留1m宽的通道,与前侧内墙保留3m宽的空地.当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
某部队驻扎在青藏高原上,那里海拔高、寒冷缺氧、四季风沙、没有新鲜蔬菜,生活条件极为艰苦.但战士们不计个人得失,扎根风雪高原,以钢铁般的意志,自力更生,克服恶劣的自然环境.该部队现计划建造一个室内面积为800m2的矩形蔬菜温室,在温室内,与左、右两侧及后侧的内墙各保留1m宽的通道,与前侧内墙保留3m宽的空地.当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?