题目内容
10.设函数g(x)=$\frac{1+sinx-cosx}{x}$(0<x≤π),求:(1)g′(x),(x2g′(x)+1)′;
(2)分别求满足(x2g′(x)+1)′≥0,(x2g′(x)+1)′<0的x的范围.
分析 (1)根据导数的运算法则,求出g(x)的导数即可,求出x2g′(x)+1的表达式,从而求出其导数即可;
(2)先求出(x2g′(x)+1)′的表达式,解不等式即可.
解答 解:(1)∵g(x)=$\frac{1+sinx-cosx}{x}$(0<x≤π),
∴g′(x)=$\frac{(x+1)cosx+(x-1)sinx-1}{{x}^{2}}$,
∴(x2g′(x)+1)′
=[(x+1)cosx+(x-1)sinx]′
=cosx-(x+1)sinx+sinx+(x-1)cosx
=x(cosx-sinx).
(2)由(1)得:(x2g′(x)+1)′=x(cosx-sinx),(0<x≤π),
令x(cosx-sinx)≥0,得$\sqrt{2}$xsin(x-$\frac{π}{4}$)≤0,解得:0<x≤$\frac{π}{4}$,
令x(cosx-sinx)<0,得$\sqrt{2}$xsin(x-$\frac{π}{4}$)>0,解得:$\frac{π}{4}$<x<π.
点评 本题考查了求函数的导数问题,考查解三角函数的不等式问题,是一道中档题.

练习册系列答案
相关题目
20.下列函数中,在区间(-1,$\frac{π}{2}$)上单调递减的函数为( )
| A. | y=x2 | B. | y=3x-1 | C. | y=log2(x+1) | D. | y=-sinx |
1.某几何体的三视图如图所示,它的表面积为( )


| A. | 3+$\frac{π}{4}$ | B. | $\frac{5π}{4}$ | C. | $\frac{7π}{8}$ | D. | π |
2.直线l与平面α垂直的一个充分条件是( )
| A. | l垂直于平面α内的一条直线 | B. | l垂直于平面α内的两条直线 | ||
| C. | l垂直于平面α内的无数条直线 | D. | l垂直于平面α内的任一条直线 |
19.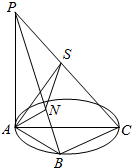 如图,AC为圆O的直径,B为圆周上不与点A、C重合的点,PA垂直于圆O所在的平面,连结PB、PC、AB、BC,作AN⊥PB,AS⊥PC,连结SN,则图中直角三角形个数为( )
如图,AC为圆O的直径,B为圆周上不与点A、C重合的点,PA垂直于圆O所在的平面,连结PB、PC、AB、BC,作AN⊥PB,AS⊥PC,连结SN,则图中直角三角形个数为( )
 如图,AC为圆O的直径,B为圆周上不与点A、C重合的点,PA垂直于圆O所在的平面,连结PB、PC、AB、BC,作AN⊥PB,AS⊥PC,连结SN,则图中直角三角形个数为( )
如图,AC为圆O的直径,B为圆周上不与点A、C重合的点,PA垂直于圆O所在的平面,连结PB、PC、AB、BC,作AN⊥PB,AS⊥PC,连结SN,则图中直角三角形个数为( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
20.已知抛物线C:y2=2px(p>0),直线l与抛物线C交于A,B两点(不同于原点),以AB为直径的圆过坐标原点O,则关于直线l的判断正确的是( )
| A. | 过定点(4p,0) | B. | 过定点(2p,0) | C. | 过定点(p,0) | D. | 过抛物线焦点 |
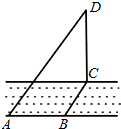 如图,在河的一侧有一塔CD=12m,河宽BC=3m,另一侧有点A,AB=4m,则点A与塔顶D的距离AD=13.
如图,在河的一侧有一塔CD=12m,河宽BC=3m,另一侧有点A,AB=4m,则点A与塔顶D的距离AD=13.