如图.在河的一侧有一塔CD=12m.河宽BC=3m.另一侧有点A.AB=4m.则点A与塔顶D的距离AD=13．题目和参考答案——青夏教育精英家教网—

题目内容

5．

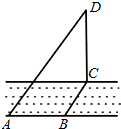如图，在河的一侧有一塔CD=12m，河宽BC=3m，另一侧有点A，AB=4m，则点A与塔顶D的距离AD=13．

分析连结AC，利用勾股定理求出AC，再计算AD．

解答解：连结AC，在Rt△ABC中，AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{16+9}$=5．
在Rt△ACD中，AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=$\sqrt{25+144}$=13．
故答案为：13．

点评本题考查了勾股定理的应用，属于基础题．

练习册系列答案

$\overrightarrow{{D_1}{B_1}}$

B．

$\overrightarrow{{D_1}B}$

C．

$\overrightarrow{D{B_1}}$

D．

$\overrightarrow{B{D_1}}$

16．已知函数f（x）=x³-ax-1．
（1）是否存在a．使f（x）的单调减区间是（-1，1）？
（2）若f（x）在R上是增函数．求a的取值范围．

13．

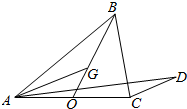如图，在△ABC中，BO为边AC上的中线，$\overrightarrow{BG}=2\overrightarrow{GO}$，设$\overrightarrow{CD}$∥$\overrightarrow{AG}$，若$\overrightarrow{AD}=\frac{1}{5}\overrightarrow{AB}+λ\overrightarrow{AC}$（λ∈R），则λ的值为（　　）

20．在如下程序框图中，已知f₀（x）=sinx，则输出的结果是（　　）

10．设函数g（x）=$\frac{1+sinx-cosx}{x}$（0＜x≤π），求：
（1）g′（x），（x²g′（x）+1）′；
（2）分别求满足（x²g′（x）+1）′≥0，（x²g′（x）+1）′＜0的x的范围．

17．比较${∫}_{0}^{3}$$\sqrt{5-\frac{5}{9}{x}^{2}}$dx与${∫}_{0}^{3}$$\sqrt{3-\frac{1}{3}{x}^{2}}$dx的大小．

14．已知a∈（$\frac{2}{3}$，1），函数f（x）=x³-$\frac{3}{2}$ax²+b，x∈[-1，1]，f（x）${\;}_{{\;}_{min}}$=1，f（x）_max=$\frac{\sqrt{6}}{2}$，求a，b的值．

15．（1）等差数列{a_n}中，a₅=11，a₈=5，求该数列的通项公式；
（2）已知等差数列{a_n}中，a₁=2，a₂和a₃是两个连续正整数的平方，求该数列的通项公式．

试题分类