题目内容
“sinα＞0”是“α为锐角”的（ ）
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：“α为锐角”，则α为第一象限角，反之α可为第一象限角，但α不一定为锐角，故可判断．
解答：
解：若“α为锐角”，则α为第一象限角，所以“sinα＞0”，成立，
反之，若“sinα＞0”，则α可为第一象限角，但α不一定为锐角，
故“sinα＞0”是“α为锐角”的必要不充分条件．
故选C．
反之，若“sinα＞0”，则α可为第一象限角，但α不一定为锐角，
故“sinα＞0”是“α为锐角”的必要不充分条件．
故选C．
点评：本题考查的重点是充要条件的判断，解题的关键是搞清锐角与第一象限角的关系．
练习册系列答案
相关题目
已知函数f（x）=sin（ωx+φ）（ω＞0，|φ|≤
）的部分图象如图所示，则f（
）=（ ）
| π |
| 2 |
| π |
| 2 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
已知数列{an}，an=-2n2+λn，若该数列是递减数列，则实数λ的取值范围是（ ）
| A、（-∞，6） |
| B、（-∞，4] |
| C、（-∞，5） |
| D、（-∞，3] |
设函数f（x）=sin（2x+φ）（0＜φ＜π），f（x）图象的一条对称轴是x=
，则φ的值为（ ）
| π |
| 8 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f（x）=3ex-x2ex-a在R上存在三个零点，则实数a的取值范围为（ ）
| A、[6e-3，2e] |
| B、（0，2e] |
| C、（-6e-3，0） |
| D、（-6e-3，2e） |
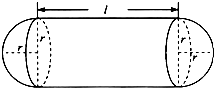某企业拟建造如图所示的容器（不计厚度，长度单位：米），其中容器的中间为圆柱形，左右两端均为半球形，按照设计要求容器的容积为
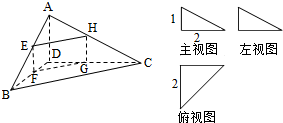四面体ABCD及其三视图如图所示，平行于棱AD，BC的平面分别交四面体的棱AB、BD、DC、CA于点E、F、G、H．