题目内容
设曲线C1的参数方程为
(t为参数),曲线C2的极坐标方程为ρ=2
sinθ,则曲线C1与C2交点的个数为( )
|
| 2 |
| A、0 | B、1 | C、2 | D、1或2 |
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:把参数方程、极坐标方程化为直角坐标方程,利用点到直线的距离公式的求出圆心到直线的距离小于半径,可得直线和圆相交,从而得出结论.
解答:
解:曲线C1的参数方程为
(t为参数)消去参数,化为直角坐标方程为 y=x+
.
曲线C2的极坐标方程为ρ=2
sinθ,即ρ2=2
ρsinθ,即 x2+(y-
)2=2,
表示圆心为(0,
)、半径等于
的圆.
由于圆心(0,
)到直线的距离d=
=<
=r,
则曲线C1与C2交点个数为2,
故选:C.
|
| 3 |
曲线C2的极坐标方程为ρ=2
| 2 |
| 2 |
| 2 |
表示圆心为(0,
| 2 |
| 2 |
由于圆心(0,
| 2 |
|0-
| ||||
|
| 2 |
则曲线C1与C2交点个数为2,
故选:C.
点评:本题主要考查把参数方程、极坐标方程化为直角坐标方程的方法,点到直线的距离公式的应用,直线和圆的位置关系,属于基础题.

练习册系列答案
相关题目
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|≤
)的部分图象如图所示,则f(
)=( )

| π |
| 2 |
| π |
| 2 |

A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
已知函数f(x)=3ex-x2ex-a在R上存在三个零点,则实数a的取值范围为( )
| A、[6e-3,2e] |
| B、(0,2e] |
| C、(-6e-3,0) |
| D、(-6e-3,2e) |
已知函数f(x+
)为奇函数,设g(x)=f(x)+1,则g(
)+g(
)+g(
)+g(
)+…+g(
)=( )
| 1 |
| 2 |
| 1 |
| 2015 |
| 2 |
| 2015 |
| 3 |
| 2015 |
| 4 |
| 2015 |
| 2014 |
| 2015 |
| A、1007 | B、2014 |
| C、2015 | D、4028 |
已知数列{an}的前n项和Sn=n2-2n,令bn=ancos
,记数列{bn}的前n项和为Tn,则T2014=( )
| nπ |
| 2 |
| A、-2011 |
| B、-2012 |
| C、-2013 |
| D、-2014 |
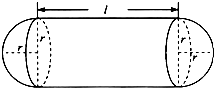 某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的容积为
某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的容积为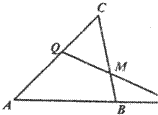 如图,在△ABC中,
如图,在△ABC中,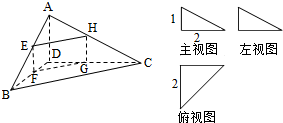 四面体ABCD及其三视图如图所示,平行于棱AD,BC的平面分别交四面体的棱AB、BD、DC、CA于点E、F、G、H.
四面体ABCD及其三视图如图所示,平行于棱AD,BC的平面分别交四面体的棱AB、BD、DC、CA于点E、F、G、H.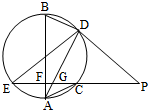 如图,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.
如图,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.