如图.已知正方体ABCD-A1B1C1D1的棱长为2.点E为线段A1B1的中点.点F.G分别是线段A1D与BC1上的动点.当三棱锥E-FGC的俯视图的面积最大时.该三棱锥的正视图的面积是2．题目和参考答案——青夏教育精英家教网——

题目内容

5．

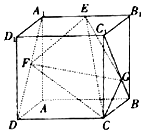如图，已知正方体ABCD-A₁B₁C₁D₁的棱长为2，点E为线段A₁B₁的中点，点F，G分别是线段A₁D与BC₁上的动点，当三棱锥E-FGC的俯视图的面积最大时，该三棱锥的正视图的面积是2．

分析由已知结合三棱锥E-FGC的俯视图的面积最大确定F、G的位置，作出三棱锥E-FGC的正视图，则面积可求．

解答解：∵E在底面ABCD上的投影为AB中点，E′，C在底面ABCD上的投影为C点本身，
F的投影在边AD上，G的投影在边BC上，如图：

要使三棱锥E-FGC的俯视图的面积最大，则F与D重合，G与B重合．
则三棱锥E-FGC的正视图为等腰三角形EAB，底边长为2，底边上的高为2．
∴面积S=$\frac{1}{2}×2×2=2$．
故答案为：2．

点评本题考查空间几何体的三视图，考查空间想象能力和思维能力，是中档题．

练习册系列答案

练习新方案系列答案

新评价单元检测创新评价系列答案

新课标单元测试卷系列答案

形成性练习与检测系列答案

形成性自主评价系列答案

南方新课堂金牌学案系列答案

挑战100单元检测试卷系列答案

金版新学案系列答案

优加全能大考卷系列答案

最新AB卷系列答案

相关题目

《九章算术》中，将底面是直角三角形的直三棱柱称为“堑堵”，已知某“堑堵”的三视图如图所示，俯视图中虚线平分矩形的面积，则该“堑堵”外接球的体积为$\frac{8\sqrt{2}π}{3}$．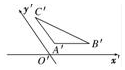

如图是三角形ABC的直观图，△ABC平面图形是直角三角形（填正三角形、锐角三角形、钝角三角形、直角三角形或者等腰三角形）

13．在△ABC中，角A，B，C的对边分别是a，b，c，且满足（2a-c）cos B=bcos C．
（1）求角B的大小；
（2）若$a=c=\sqrt{3}$，求b的值．

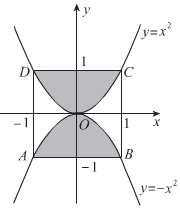如图正方形的四个顶点A（-1，-1），B（1，-1），C（1，1），D（-1，1）分别在抛物线y=-x²和y=x²上，求阴影区域的面积．

10．祖暅著《缀术》有云：“缘幂势既同，则积不容异”，这就是著名的祖暅原理，如图1，现有一个半径为R的实心球，以该球某条直径为中心轴挖去一个半径为r的圆柱形的孔，再将余下部分熔铸成一个新的实心球，则新实心球的半径为$\root{3}{\frac{2{R}^{3}-3{r}^{2}\sqrt{{R}^{2}-{r}^{2}}}{2}}$（如图2，势为h时幂为S=π（R²-r²-h²））

17．已知复数z满足i（z+1）=-2+2i（i是虚数单位）
（1）求z的虚部；
（2）若$ω=\frac{z}{1-2i}$，求|ω|²⁰¹⁵．

14．在平面直角坐标系中，直线l的参数方程为$\left\{\begin{array}{l}x=t+1\\ y=\sqrt{3}t+1\end{array}\right.$（t为参数），以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为3ρ²cos²θ+4ρ²sin²θ=12．
（Ⅰ）写出直线l的极坐标方程与曲线C的直角坐标方程；
（Ⅱ）已知与直线l平行的直线l'过点M（1，0），且与曲线C交于A，B两点，试求|AB|．

15．某几何体的三视图如图所示，则该几何体的表面积为（　　）