题目内容
1.绘制以下算法对应的程序框图:第一步,输入变量x;
第二步,根据函数f(x)=$\left\{\begin{array}{l}{5-x(x≥2)}\\{3(-2≤x<2)}\\{4+3x(x<-2)}\end{array}\right.$
对变量y赋值,使y=f(x);
第三步,输出变量y的值.
分析 该函数是分段函数,当x取不同范围内的值时,函数解析式不同,因此当给出一个自变量x的值时,必须先判断x 的范围,然后确定利用哪一段的解析式求函数值,因为函数解析式分了三段,所以判断框需要两个,即进行两次判断,于是,即可画出相应的程序框图.
解答 解:程序框图如下: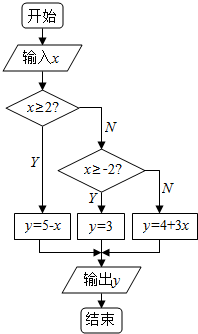
点评 画程序框图的规则:
(1)使用标准的框图符号;
(2)框图一般按从上到下、从左到右的方向画;
(3)除判断框外,大多数程序框图中的程序框只有一个进入点和一个退出点,判断框是具有超过一个退出点的唯一符号;
(4)在图形符号内描述的语言要非常简练清楚.
程序框图有以下重要的结构:顺序结构、条件结构、循环结构.

练习册系列答案
相关题目
12.某大学进行自主招生时,需要进行逻辑思维和阅读表达两项能力的测试.学校对参加测试的200名学生的逻辑思维成绩、阅读表达成绩以及这两项的总成绩进行了排名.其中甲、乙、丙三位同学的排名情况如图所示:

下列叙述一定正确的是( )

下列叙述一定正确的是( )
| A. | 甲同学的阅读表达成绩排名比他的逻辑思维成绩排名更靠前 | |
| B. | 乙同学的逻辑思维成绩排名比他的阅读表达成绩排名更靠前 | |
| C. | 甲、乙、丙三位同学的逻辑思维成绩排名中,甲同学更靠前 | |
| D. | 乙同学的总成绩排名比丙同学的总成绩排名更靠前 |
9.已知矩形ABCD的顶点都在半径为5的球P的球面上,且AB=4,BC=3,则棱锥P-ABCD的体积为( )
| A. | 5$\sqrt{3}$ | B. | 30$\sqrt{3}$ | C. | $\frac{{10\sqrt{3}}}{3}$ | D. | 10$\sqrt{3}$ |
16.将八进制数26(8)转化为十进制数,结果是( )
| A. | 20 | B. | 22 | C. | 24 | D. | 26 |
6.已知各项为正的数列{an}的前n项的乘积为Tn,点(Tn,n2-15n)在函数y=${log}_{\frac{1}{2}}$x的图象上,则数列{log2an}的前10项和为( )
| A. | -140 | B. | 50 | C. | 124 | D. | 156 |
10.m<n<0是$\frac{1}{m}$>$\frac{1}{n}$成立的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |