题目内容
17.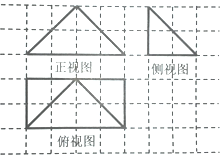 某几何体的三视图如图所示(网络中每个小正方形的边长为1),若这个几何体的顶点都在球O的表面上,则这个球的表面积是( )
某几何体的三视图如图所示(网络中每个小正方形的边长为1),若这个几何体的顶点都在球O的表面上,则这个球的表面积是( )| A. | 20π | B. | 4$\sqrt{5}$π | C. | $\frac{49π}{16}$ | D. | $\frac{49π}{4}$ |
分析 由三视图画出直观图,有题意求得外接球的直径D,球O的表面积是4π×($\sqrt{5}$)2=20π.
解答  解:由三视图得原直观图如图,原几何体为三棱锥A-BCD,满足AD⊥底面BCD,底面BDC为等腰直角三角形,
解:由三视图得原直观图如图,原几何体为三棱锥A-BCD,满足AD⊥底面BCD,底面BDC为等腰直角三角形,
则该几何体的外接球即为以DA、DB、DC为棱的长方体的外接球,外接球的直径D满足D2=DA2+DB2+DC2=4+8+8=20,
∴外接球O的半径为$\frac{1}{2}$D=$\sqrt{5}$,
∴球O的表面积是4π×($\sqrt{5}$)2=20π.
故选:A.
点评 本题考查三视图的应用,四面体外接球的求法,考查数形结合思想,属于中档题.

练习册系列答案
相关题目
7.已知复数z的实部和虚部相等,且z(2+i)=3-bi(b∈R),则|z|=( )
| A. | 3$\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 3 | D. | 2 |
12.已知i是虚数单位,设1+ai=$\frac{2+bi}{i}$(a、b为实数),则a+bi在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
8.若x、y满足x2+y2-2x+4y-20=0,则x2+y2的最小值是( )
| A. | $\sqrt{5}$-5 | B. | 5-$\sqrt{5}$ | C. | 30-10$\sqrt{5}$ | D. | 无法确定 |
 如图是半径分别为1,2,3的三个同心圆,现随机向最大圆内抛一粒豆子,则豆子落入图中阴影部分的概率为$\frac{1}{3}$.
如图是半径分别为1,2,3的三个同心圆,现随机向最大圆内抛一粒豆子,则豆子落入图中阴影部分的概率为$\frac{1}{3}$.