题目内容
8．若x、y满足x2+y2-2x+4y-20=0，则x2+y2的最小值是（ ）| A． | $\sqrt{5}$-5 | B． | 5-$\sqrt{5}$ | C． | 30-10$\sqrt{5}$ | D． | 无法确定 |
分析 把圆的方程化为标准方程后，找出圆心坐标和圆的半径r，设圆上一点的坐标为（x，y），原点坐标为（0，0），则x2+y2表示圆上一点和原点之间的距离的平方，根据图象可知此距离的最小值为圆的半径r减去圆心到原点的距离，利用两点间的距离公式求出圆心到原点的距离，利用半径减去求出的距离，然后平方即为x2+y2的最小值．
解答 
解：把圆的方程化为标准方程得：
（x-1）2+（y+2）2=25，则圆心A坐标为（1，-2），圆的半径r=5，
设圆上一点的坐标为（x，y），原点O坐标为（0，0），
则|AO|=$\sqrt{5}$，|AB|=r=5，
所以|BO|=|AB|-|OA|=5-$\sqrt{5}$．
则x2+y2的最小值为（5-$\sqrt{5}$）2=30-10$\sqrt{5}$．
故选C．
点评 此题考查学生会把圆的一般方程化为圆的标准方程并会由圆的标准方程找出圆心坐标与半径，考查了数形结合的数学思想，是一道中档题．
练习册系列答案
相关题目
17．
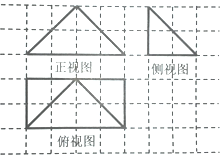某几何体的三视图如图所示（网络中每个小正方形的边长为1），若这个几何体的顶点都在球O的表面上，则这个球的表面积是（ ）
某几何体的三视图如图所示（网络中每个小正方形的边长为1），若这个几何体的顶点都在球O的表面上，则这个球的表面积是（ ）| A． | 20π | B． | 4$\sqrt{5}$π | C． | $\frac{49π}{16}$ | D． | $\frac{49π}{4}$ |
13．若将函数y=3cos（2x+$\frac{π}{2}$）的图象向右平移$\frac{π}{6}$个单位长度，则平移后图象的一个对称中心是（ ）
| A． | （$\frac{π}{6}$，0） | B． | （-$\frac{π}{6}$，0） | C． | （$\frac{π}{12}$，0） | D． | （-$\frac{π}{12}$，0） |
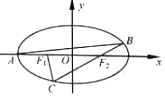如图，设点A，F1，F2分别为椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$的左顶点和左，右焦点，过点A作斜率为k的直线交椭圆于另一点B，连接BF2并延长交椭圆于点C．