题目内容
12．已知i是虚数单位，设1+ai=$\frac{2+bi}{i}$（a、b为实数），则a+bi在复平面内对应的点在（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 把已知等式变形，利用复数相等的条件列式求得a，b的值，则答案可求．
解答 解：由1+ai=$\frac{2+bi}{i}$，得-a+i=2+bi，
∴$\left\{\begin{array}{l}{-a=2}\\{1=b}\end{array}\right.$，即$\left\{\begin{array}{l}{a=-2}\\{b=1}\end{array}\right.$，
∴a+bi在复平面内对应的点坐标为（-2，1），
即该点位于第二象限．
故选：B．
点评 本题考查复数代数形式的乘除运算，考查了复数相等的条件，是基础题．
练习册系列答案
相关题目
20．已知实数x，y满足约束条件$\left\{\begin{array}{l}x-y≥0\\ x+2y≤4\\ x-2y≤2\end{array}\right.$，则目标函数z=x+3y的最大值为（ ）
| A． | $\frac{16}{3}$ | B． | $\frac{9}{2}$ | C． | -8 | D． | $\frac{17}{2}$ |
17．
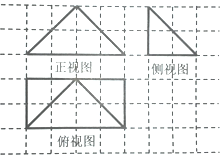某几何体的三视图如图所示（网络中每个小正方形的边长为1），若这个几何体的顶点都在球O的表面上，则这个球的表面积是（ ）
某几何体的三视图如图所示（网络中每个小正方形的边长为1），若这个几何体的顶点都在球O的表面上，则这个球的表面积是（ ）| A． | 20π | B． | 4$\sqrt{5}$π | C． | $\frac{49π}{16}$ | D． | $\frac{49π}{4}$ |
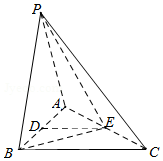如图：等边三角形PAB所在的平面与Rt△ABC所在的平面互相垂直，D、E分别为AB、AC边中点．已知AB⊥BC，AB=2，BC=2$\sqrt{3}$