题目内容
7.已知复数z的实部和虚部相等,且z(2+i)=3-bi(b∈R),则|z|=( )| A. | 3$\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 3 | D. | 2 |
分析 把已知等式变形,利用复数代数形式的乘除运算化简,再由实部和虚部相等求得b,得到z,代入复数模的计算公式得答案.
解答 解:由z(2+i)=3-bi,得$z=\frac{3-bi}{2+i}=\frac{(3-bi)(2-i)}{(2+i)(2-i)}$=$\frac{6-b-(2b+3)i}{5}$,
∴6-b=-2b-3,解得b=-9.
∴z=3+3i,
则|z|=$\sqrt{{3}^{2}+{3}^{2}}=3\sqrt{2}$.
故选:A.
点评 本题考查复数代数形式的乘除运算,考查了复数模的求法,是基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
17.从1,2,3,4,5这5个数字中任取3个数字组成没有重复数字的三位数,则这个三位数是偶数的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{5}$ |
17.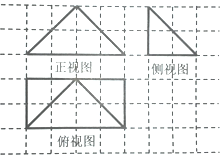 某几何体的三视图如图所示(网络中每个小正方形的边长为1),若这个几何体的顶点都在球O的表面上,则这个球的表面积是( )
某几何体的三视图如图所示(网络中每个小正方形的边长为1),若这个几何体的顶点都在球O的表面上,则这个球的表面积是( )
 某几何体的三视图如图所示(网络中每个小正方形的边长为1),若这个几何体的顶点都在球O的表面上,则这个球的表面积是( )
某几何体的三视图如图所示(网络中每个小正方形的边长为1),若这个几何体的顶点都在球O的表面上,则这个球的表面积是( )| A. | 20π | B. | 4$\sqrt{5}$π | C. | $\frac{49π}{16}$ | D. | $\frac{49π}{4}$ |