题目内容
若方程kx-lnx=0有两个实数根,则k的取值范围是 .
考点:根的存在性及根的个数判断,对数函数的图像与性质
专题:计算题,作图题,函数的性质及应用
分析:方程kx-lnx=0有两个实数根可化为函数y=kx与函数y=lnx有两个不同的交点,作函数的图象求解.
解答:
解:方程kx-lnx=0有两个实数根可化为
函数y=kx与函数y=lnx有两个不同的交点,
作函数y=kx与函数y=lnx的图象如下,

结合图象知,
当直线与y=lnx相切时,设切点为(x,lnx);
故
=
;
故x=e;
故直线的斜率k=
;
故k的取值范围为(0,
).
故答案为:(0,
).
函数y=kx与函数y=lnx有两个不同的交点,
作函数y=kx与函数y=lnx的图象如下,

结合图象知,
当直线与y=lnx相切时,设切点为(x,lnx);
故
| lnx |
| x |
| 1 |
| x |
故x=e;
故直线的斜率k=
| 1 |
| e |
故k的取值范围为(0,
| 1 |
| e |
故答案为:(0,
| 1 |
| e |
点评:本题考查了方程的根与函数的图象的应用,属于基础题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
在△ABC中,tanA是以-4为第三项,4为第七项的等差数列的公差,tanB是以
为第三项,9为第六项的等比数列公比,则这个三角形是( )
| 1 |
| 3 |
| A、钝角三角形 |
| B、锐角三角形 |
| C、等腰直角三角形 |
| D、以上都不对 |
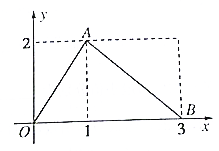 函数y=f(x)的图象是如图所示的折线段OAB,已知点A坐标为(1,2)点B的坐标为(3,0),若P(x,y)是函数g(x)=f(x)(x-1)图象上的动点,则x+y的最大值为( )
函数y=f(x)的图象是如图所示的折线段OAB,已知点A坐标为(1,2)点B的坐标为(3,0),若P(x,y)是函数g(x)=f(x)(x-1)图象上的动点,则x+y的最大值为( )A、
| ||
| B、2 | ||
C、
| ||
| D、4 |
若sinx-sin(
-x)=
,则tanx+
的值是( )
| 3π |
| 2 |
| 2 |
| 1 |
| tan(x-π) |
| A、2 | B、-1 | C、1 | D、2 |