题目内容
已知单调递增的等比数列{an}中,a2+a3+a4=28,且a3+2是a2,a4的等差中项,
(1)求an
(2)设bn=log
an,Sn=b1+b2+…+bn,求Sn.
(1)求an
(2)设bn=log
| 1 |
| 2 |
考点:数列的求和,等差数列与等比数列的综合
专题:等差数列与等比数列
分析:(1)设等比数列{an}的公比是q,利用等比数列的通项公式和等差中项的性质列出方程,结合条件求出等比数列的首项、公比,再求出an;
(2)由(1)和对数的运算求出bn,利用等差数列的前n项和公式求出Sn.
(2)由(1)和对数的运算求出bn,利用等差数列的前n项和公式求出Sn.
解答:
解:(1)设等比数列{an}的公比是q,
因为a2+a3+a4=28,且a3+2是a2,a4的等差中项,
所以
,解得
或
,
因为等比数列{an}是递增数列,所以
,
则an=2•2n-1=2n;
(2)由(1)得,bn=log
an=bn=log
2n=-n,
所以Sn=b1+b2+…+bn=-(1+2+3+…+n)=-
,
即Sn=-
.
因为a2+a3+a4=28,且a3+2是a2,a4的等差中项,
所以
|
|
|
因为等比数列{an}是递增数列,所以
|
则an=2•2n-1=2n;
(2)由(1)得,bn=log
| 1 |
| 2 |
| 1 |
| 2 |
所以Sn=b1+b2+…+bn=-(1+2+3+…+n)=-
| n(1+n) |
| 2 |
即Sn=-
| n(1+n) |
| 2 |
点评:本题考查等比数列的通项公式,等差中项的性质,以及等差数列的前n项和公式,考查方程思想和计算能力.

练习册系列答案
相关题目
极坐标方程ρ=
化为普通方程是( )
| 2 |
| 1+cosθ |
| A、y2=4(x-1) |
| B、y2=4(1-x) |
| C、y2=2(x-1) |
| D、y2=2(1-x) |
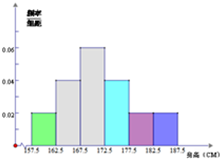 云南省2014年全省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布N(107.5,16).现从我校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第一组[157.5,162.5],第二组[162.5,167.5],…,第6组[182.5,187.5],如图是按上述分组方法得到的频率分布直方图.
云南省2014年全省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布N(107.5,16).现从我校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第一组[157.5,162.5],第二组[162.5,167.5],…,第6组[182.5,187.5],如图是按上述分组方法得到的频率分布直方图.