题目内容
已知随机变量ξ+η=8,若ξ~B(2,0.35),则E(η),D(η)分别是 , .
考点:离散型随机变量的期望与方差
专题:概率与统计
分析:根据变量ξ~B(2,0.35),可以根据公式做出这组变量的均值与方差,随机变量ξ+η=8,知道变量η也符合二项分布,故可得结论.
解答:
解:∵ξ~B(2,0.35),
∴Eξ=2×0.35=0.7,Dξ=2×0.35×0.65=0.425,
∵ξ+η=8,
∴Eη=E(8-ξ)=7.3,Dη=D(8-ξ)=0.425,
故答案为:7.3,0.425.
∴Eξ=2×0.35=0.7,Dξ=2×0.35×0.65=0.425,
∵ξ+η=8,
∴Eη=E(8-ξ)=7.3,Dη=D(8-ξ)=0.425,
故答案为:7.3,0.425.
点评:本题考查变量的极值与方差,均值反映数据的平均水平,而方差反映数据的波动大小,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
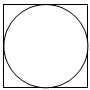 一次实验:向如图所示的正方形中随机撒一大把豆子,经查数,落在正方形中的豆子的总数为N粒,其中m(m<N)粒豆子落在该正方形的内切圆内,以此估计圆周率π为( )
一次实验:向如图所示的正方形中随机撒一大把豆子,经查数,落在正方形中的豆子的总数为N粒,其中m(m<N)粒豆子落在该正方形的内切圆内,以此估计圆周率π为( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知cos(α-
)+sinα=
,且α∈(0,
)则sin(α+
π)的是( )
| π |
| 6 |
| 4 |
| 5 |
| 3 |
| π |
| 3 |
| 5 |
| 12 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f(x)=
.设a=log
,则f(f(a))的值等于( )
|
| 1 |
| 2 |
| 3 |
A、
| ||
| B、2 | ||
| C、3 | ||
| D、-2 |
将函数y=sin2x的图象向右平移
个单位,得到y=cos(2x+φ),φ∈(-π,π]的图象,则φ的值为( )
| π |
| 6 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|