题目内容
将函数y=sin2x的图象向右平移
个单位,得到y=cos(2x+φ),φ∈(-π,π]的图象,则φ的值为( )
| π |
| 6 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:求出变换后的函数的解析式,将两个函数化为同名函数,得到所求函数,即可求出φ的值.
解答:
解:∵函数y=sin2x=cos(2x-
)=cos2(x-
),
将函数y=sin2x的图象向右平移
个单位,得到y=cos2(x-
-
)=cos(2x-
),
即得到y=cos(2x+φ),φ∈(-π,π]的图象.
∴φ=-
.
故选:D.
| π |
| 2 |
| π |
| 4 |
将函数y=sin2x的图象向右平移
| π |
| 6 |
| π |
| 6 |
| π |
| 4 |
| 5π |
| 6 |
即得到y=cos(2x+φ),φ∈(-π,π]的图象.
∴φ=-
| 5π |
| 6 |
故选:D.
点评:本题考查函数图象的平移,实质上是点的平移,点的位置改变引起所在图形的位置改变,而形状大小没有改变,但函数的解析式发生变化.要提醒学生注意平移方向.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
若x>1,则x+
的最小值是( )
| 1 |
| x-1 |
| A、1 | B、2 | C、3 | D、4 |
在各项均为正的数列{an}中,已知2an=3an+1,a2•a5=
,则通项an为( )
| 8 |
| 27 |
A、(
| ||
B、(
| ||
C、(
| ||
D、(
|
已知cos(α+
)=
,α∈(-
,0),则tan(2π-α)=( )
| π |
| 2 |
| 2 |
| 3 |
| π |
| 2 |
A、±
| ||||
B、
| ||||
C、-
| ||||
D、
|
设命题p:平面α∩平面β=l,若m⊥l,则m⊥β;命题q:函数y=cos(x-
)的图象关于直线x=
对称.则下列判断正确的是( )
| π |
| 2 |
| π |
| 2 |
| A、p为真 | B、¬q为假 |
| C、p∨q为假 | D、p∧q为真 |
 如图,在等腰直角△ABC中,AB=AC=3,点D在边BC上且BD=
如图,在等腰直角△ABC中,AB=AC=3,点D在边BC上且BD=| 1 |
| 2 |
| AP |
| CP |
A、[-
| ||
B、[-
| ||
C、[
| ||
D、[0,
|
一个几何体的三视图如图所示,则该几何体的体积为( )


| A、55 | ||
| B、54 | ||
C、75+4
| ||
D、55+2
|
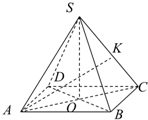 如图,设S-ABCD是一个高为3的四棱锥,底面ABCD是边长为2的正方形,顶点S在底面上的射影是正方形ABCD的中心.K是棱SC的中点.试求直线AK与平面SBC所成角的大小.
如图,设S-ABCD是一个高为3的四棱锥,底面ABCD是边长为2的正方形,顶点S在底面上的射影是正方形ABCD的中心.K是棱SC的中点.试求直线AK与平面SBC所成角的大小.