题目内容
求过点P(0,1)的直线l,使它包含在两已知直线l1:2x+y-8=0和l2:x-3y+10=0间的线段被点P平分.
考点:直线的点斜式方程
专题:直线与圆
分析:根据题意,设出直线l1上的一点P1,求出P1关于点P的对称点P2;由P2在直线l2上,求出点P1,即得所求的直线方程.
解答:
解:根据题意,直线l1:2x+y-8=0可化为
y=-2x+8;
设直线l1上的一点P1(x1,-2x1+8),
则P1关于点P的对称点是P2(-x1,2-(-2x1+8));
P2在直线l2:x-3y+10=0上,
即-x1-3(2x1-6)+10=0,
解得x1=4,
∴y1=0;
∴所求的直线方程是
+y=1,即x+4y-4=0.
y=-2x+8;
设直线l1上的一点P1(x1,-2x1+8),
则P1关于点P的对称点是P2(-x1,2-(-2x1+8));
P2在直线l2:x-3y+10=0上,
即-x1-3(2x1-6)+10=0,
解得x1=4,
∴y1=0;
∴所求的直线方程是
| x |
| 4 |
点评:本题考查了求直线方程的问题,解题时应根据题意,挖掘解题条件,利用对称关系,求出所求直线上的另一点,是易错题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
若[x]表示不超过x的最大整数,如[-2.4]=-3,[3.14]=3,定义函数f(x)=[x[x]],当x∈[0,n)(n∈N*且N≥2)时,设函数f(x)的值域为集合A,记A中的元素个数为an,则
的最小值为( )
| 2an+n+7 |
| n |
A、
| ||
| B、6 | ||
C、
| ||
| D、以上答案都不对 |
某程序框图如图所示,则该程序运行后输出的值是( )


| A、2 | B、-2 | C、3 | D、-3 |
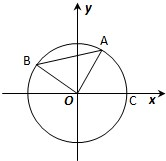 如图,A,B是单位圆O上的动点,且A,B分别在第一,二象限.C是圆与x轴的交点,△AOB为正三角形.若A点的坐标为(x,y).记∠COA=α,求|BC|2的取值范围.
如图,A,B是单位圆O上的动点,且A,B分别在第一,二象限.C是圆与x轴的交点,△AOB为正三角形.若A点的坐标为(x,y).记∠COA=α,求|BC|2的取值范围.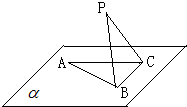 如图,△ABC在平面α内,∠ACB=90°,AB=2BC=2,P为平面α外一个动点,且PC=
如图,△ABC在平面α内,∠ACB=90°,AB=2BC=2,P为平面α外一个动点,且PC=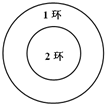 如图,一半径为
如图,一半径为